La pyramide avec un prisme est un polyèdre parfait dans un espace tridimensionnel, leurs caractéristiques géométriques sont étudiées au lycée. Dans cet article, nous examinerons ce que sont les pyramides, de quels éléments elles consistent et nous caractériserons également brièvement les pyramides correctes.
Pyramide à figures géométriques
Du point de vue de la géométrie, la pyramide est une figure spatiale composée d'un polygone et de plusieurs triangles. Obtenir ce chiffre est assez simple. Pour ce faire, prenez un polygone à n côtés, puis choisissez un point arbitraire dans l'espace qui ne se trouvera pas dans le plan du polygone, et connectez chaque sommet du polygone à ce point. De toute évidence, la figure formée de cette manière aura n triangles connectés les uns aux autres à un sommet.
Pour visualiser la forme géométrique de la figure décrite, prenons une photo.

Cela montre une pyramide quadrangulaire dont la base estquadrilatère, et la surface latérale est formée de quatre triangles qui ont un sommet commun.
Éléments de la pyramide
Comme tout polyèdre, la pyramide est formée de trois types d'éléments:
- bords;
- hauts;
- côtes.
Les visages sont des parties de plans qui séparent le volume interne d'une figure de l'espace environnant. Si la base de la pyramide contient un n-gone, alors le nombre de ses faces est toujours n+1. Parmi ceux-ci, n côtés sont triangulaires et un côté est la base n-gonale mentionnée.
Les sommets sont des points où trois faces ou plus d'une figure se croisent. La région de base contient n sommets, dont chacun est formé de deux faces triangulaires et d'une base. Le point où n côtés triangulaires se rencontrent est appelé le sommet de la pyramide. Ainsi, la figure considérée est constituée de n+1 sommets.
Les arêtes sont des lignes droites qui apparaissent lorsque deux faces se croisent. Chaque arête est délimitée par deux sommets à ses extrémités. Toute pyramide à base de n-gones contient 2n arêtes. La moitié de ce nombre, c'est-à-dire n, est formée uniquement par l'intersection de triangles latéraux.
Types de chiffres possibles
Le nom de la figure considérée est uniquement déterminé par le type de polygone à la base. Par exemple, si elle a trois coins et trois côtés, alors la pyramide sera triangulaire, si quatre - quadrangulaire, et ainsi de suite.
Le polygone peut être convexe et concave, ainsi que de type régulier et général. Tout cela détermine également l'apparence de la pyramide.
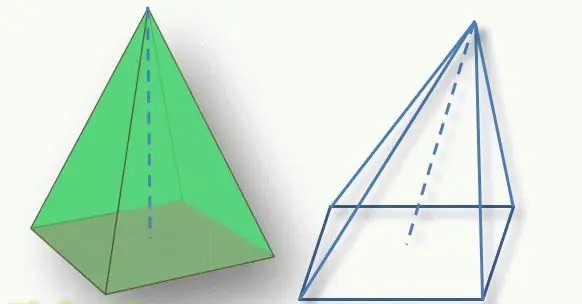
Un point important pour déterminer le type de figure est la position du sommet de la pyramide par rapport à sa base. Le segment perpendiculaire tracé du haut à la base polygonale s'appelle la hauteur de la figure. Si ce segment coupe la base en son centre géométrique (pour un triangle, c'est l'intersection des médianes, pour un quadrilatère, l'intersection des diagonales), alors la figure s'appelle une droite. Sinon, on parle de pyramide inclinée.
Si le n-gone de la base est régulier (triangle équilatéral, carré, etc.) et que la figure est droite, alors on l'appelle une pyramide régulière.
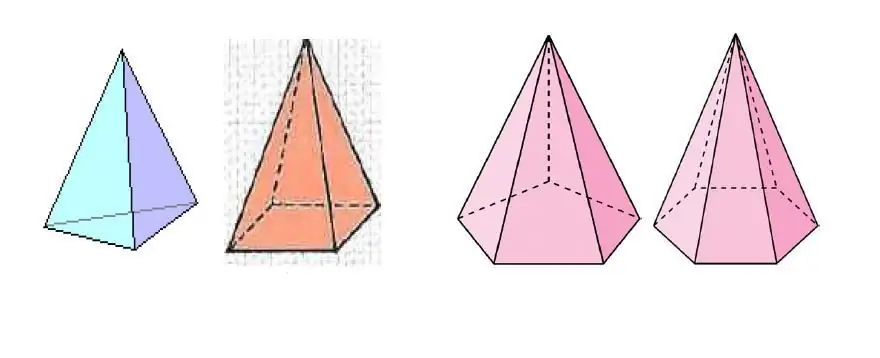
L'image ci-dessus montre plusieurs pyramides, qui diffèrent par le nombre de côtés du polygone à la base.
Propriétés des pyramides régulières
Ces pyramides diffèrent des autres figures de cette classe par un haut degré de symétrie. À cet égard, il est pratique d'effectuer divers calculs géométriques avec eux, par exemple, le volume ou la surface.
Une pyramide régulière contient un n-gone à sa base, dont l'aire est uniquement déterminée à partir de la connaissance de la longueur de son côté. La surface latérale de la figure est formée de n triangles identiques, équilatéraux. Les arêtes d'une pyramide régulière situées sur la surface latérale sont égales les unes aux autres. La valeur de la longueur de cette arête est souvent utilisée lors du calcul de l'apothème d'une figure et de la détermination de la surface.
La hauteur d'une pyramide régulière est la deuxième caractéristique importante de la figure (la première est la longueur de l'arêteterrains). La hauteur est utilisée lors du calcul du volume.
Tout plan parallèle à la base, qui coupe les faces latérales de la pyramide, conduit à la formation d'une section polygonale. Il est homothétique par rapport au polygone de base. L'opération de découpage décrite conduit à la formation de toute une classe de nouvelles figures - des pyramides régulières tronquées.
Les pyramides les plus célèbres

Bien sûr, ce sont les pyramides quadrangulaires régulières des pharaons égyptiens. Dans un endroit appelé Gizeh, il y a plus de 100 de ces monuments de pierre, dont la perfection du design et la précision des paramètres géométriques continuent d'étonner les scientifiques à ce jour. La plus grande d'entre elles est la pyramide de Khéops, qui mesure environ 146 mètres de haut et environ 230 mètres de long.
À quoi servaient exactement ces pyramides, ainsi que par quels mécanismes et quand elles ont été construites, personne ne le sait à ce jour.






