En mathématiques, la sommation (désignée par le grand symbole grec sigma) est un ensemble de sommations de nombres. Quel est le montant ? C'est le résultat d'une telle action. Si les nombres sont additionnés les uns après les autres de gauche à droite, alors le résultat intermédiaire est une somme partielle.
Quel est le montant ?
Les nombres à additionner peuvent être entiers, rationnels, réels ou complexes. En plus d'eux, d'autres types de valeurs peuvent être ajoutés: des vecteurs, des matrices, des polynômes et, en général, des éléments de tout groupe additif (ou même un monoïde).
Si le nombre d'éléments des termes est fini, alors la sommation donne toujours une valeur bien définie. La sommation d'une séquence infinie de valeurs s'appelle une série. Sa valeur peut souvent être déterminée à l'aide d'une limite (bien que parfois la valeur puisse être infinie).
Séquences
La somme des nombres [3, 7, 2, 1] peut être définie par une expression dont la valeur est la somme des chiffres qu'elle contient, par exemple 3 + 7 + 2 + 1=13. Puisque le une additionde manière associative, la somme ne dépend pas de la façon dont les termes sont regroupés, par exemple, (3 + 7) + (2 + 1) et 3 + ((7 + 2) + 1) sont tous deux égaux à neuf, donc les parenthèses sont généralement supprimées. L'addition est également commutative, donc le réarrangement des termes ne change pas la valeur de la somme. Notez que cette propriété peut ne pas fonctionner pour une sommation infinie.

Il n'y a pas de notation spéciale pour additionner des séquences de ce type. Il n'y a qu'une légère nuance s'il y a moins de deux éléments. La sommation d'une séquence d'un membre ne contient pas de signe plus (elle ne peut être distinguée de la forme du nombre lui-même), et s'il n'y a aucun élément, alors elle ne peut même pas être écrite (mais à la place, elle peut être notée par sa valeur "0"). Si, toutefois, les termes de la séquence sont spécifiés par un modèle spécifique, tel qu'une fonction, alors l'opérateur de sommation peut être utile ou même essentiel.
Enregistrer
Pour comprendre ce qu'est une somme, il faut aussi analyser son apparence.
Pour additionner une séquence d'entiers de 1 à 100, on utilise souvent une expression qui inclut des points de suspension pour indiquer les membres manquants: 1 + 2 + 3 + 4 + … + 99 + 100. Le modèle est assez facile à voir dans cet exemple. Cependant, pour des options plus complexes, il est nécessaire de préciser exactement la règle utilisée pour trouver la valeur des éléments, ce qui peut être réalisé à l'aide de l'opérateur de sommation « Σ ». A l'aide de ce symbole (sigma), vous pouvez appliquer la notation suivante:
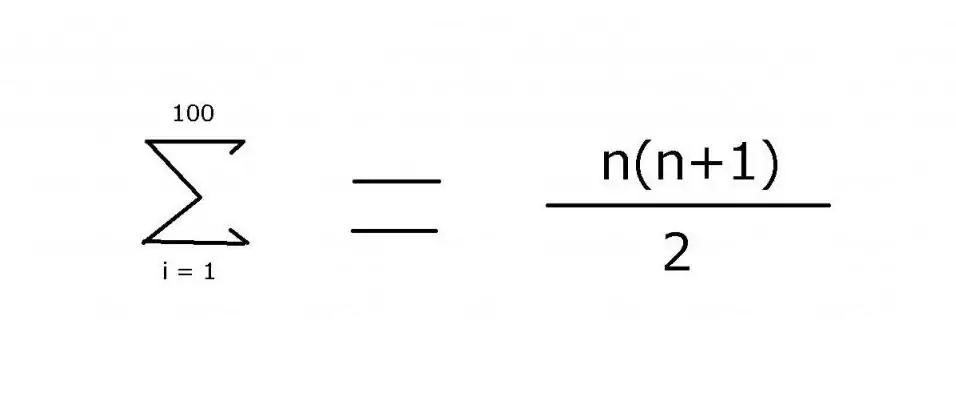
La valeur de cette expression est 5050. Elle peut être trouvée en utilisant l'induction mathématique, d'où vient la deuxième partie de la formule.
Pour différentes séquences, la formule changera. Le processus d'enregistrement se réduit à rechercher la pré-image d'une séquence infinie, puis à la décrire avec une formule. Cela fait, il n'est pas difficile de comprendre quel est le montant dans un cas particulier.
Lorsqu'il est nécessaire de préciser que les nombres sont additionnés avec leurs signes (plus ou moins), le terme somme algébrique est utilisé. Par exemple, dans la théorie des circuits électriques, les lois des circuits de Kirchhoff considèrent la somme algébrique des courants dans un réseau de conducteurs se rencontrant en un point, donnant des signes opposés aux courants entrant et sortant d'un nœud.






