Gaz parfait, l'équation d'état du gaz parfait, sa température et sa pression, son volume… la liste des paramètres et définitions utilisés dans la section de physique correspondante peut se poursuivre assez longtemps. Aujourd'hui, nous ne parlerons que de ce sujet.
Qu'est-ce qui est considéré en physique moléculaire ?

L'objet principal considéré dans cette section est un gaz parfait. L'équation d'état des gaz parfaits a été obtenue en tenant compte des conditions environnementales normales, et nous en reparlerons un peu plus tard. Abordons maintenant ce "problème" de loin.
Disons que nous avons une masse de gaz. Son état peut être déterminé à l'aide de trois paramètres de nature thermodynamique. Ce sont, bien sûr, la pression, le volume et la température. L'équation de l'état du système dans ce cas sera la formule de la relation entre les paramètres correspondants. Il ressemble à ceci: F (p, V, T)=0.
Ici, pour la première fois, nous approchons lentement de l'émergence d'une telle chose comme idéalegaz. C'est ce qu'on appelle un gaz dans lequel les interactions entre les molécules sont négligeables. En général, cela n'existe pas dans la nature. Cependant, tout gaz hautement raréfié en est proche. L'azote, l'oxygène et l'air, qui sont dans des conditions normales, diffèrent peu de l'idéal. Pour écrire l'équation d'état d'un gaz parfait, on peut utiliser la loi des gaz unifiée. On obtient: pV/T=const.
Concept associé 1: Loi d'Avogadro
Il peut nous dire que si nous prenons le même nombre de moles d'absolument n'importe quel gaz aléatoire et que nous les plaçons dans les mêmes conditions, y compris la température et la pression, alors les gaz occuperont le même volume. En particulier, l'expérience a été réalisée dans des conditions normales. Cela signifie que la température était de 273,15 Kelvin, la pression était d'une atmosphère (760 millimètres de mercure, ou 101325 Pascals). Avec ces paramètres, le gaz occupait un volume égal à 22,4 litres. Par conséquent, nous pouvons dire que pour une mole de n'importe quel gaz, le rapport des paramètres numériques sera une valeur constante. C'est pourquoi il a été décidé de désigner ce chiffre par la lettre R et de l'appeler la constante universelle des gaz. Ainsi, il est égal à 8,31. L'unité est J/molK.
Gaz idéal. L'équation d'état des gaz parfaits et sa manipulation
Essayons de réécrire la formule. Pour ce faire, on l'écrit sous cette forme: pV=RT. Ensuite, nous effectuons une action simple, multiplions les deux côtés de l'équation par un nombre arbitraire de moles. On obtient pVu=uRT. Tenons compte du fait que le produit du volume molaire etla quantité de matière est simplement le volume. Mais après tout, le nombre de moles sera simultanément égal au quotient de la masse et de la masse molaire. C'est exactement à quoi ressemble l'équation de Mendeleïev-Clapeyron. Cela donne une idée claire du type de système que forme un gaz parfait. L'équation d'état d'un gaz parfait prendra la forme: pV=mRT/M.
Déduire la formule de la pression
Faisons quelques manipulations supplémentaires avec les expressions obtenues. Pour ce faire, le côté droit de l'équation de Mendeleïev-Clapeyron est multiplié et divisé par le nombre d'Avogadro. Maintenant, nous regardons attentivement le produit de la quantité de substance par le nombre d'Avogadro. Ce n'est rien d'autre que le nombre total de molécules dans le gaz. Mais en même temps, le rapport de la constante universelle des gaz au nombre d'Avogadro sera égal à la constante de Boltzmann. Par conséquent, les formules de pression peuvent être écrites comme suit: p=NkT/V ou p=nkT. Ici, le symbole n est la concentration de particules.
Procédés de gaz idéaux
En physique moléculaire, les isoprocessus existent. Ce sont des processus thermodynamiques qui se déroulent dans le système à l'un des paramètres constants. Dans ce cas, la masse de la substance doit également rester constante. Examinons-les plus précisément. Ainsi, les lois d'un gaz parfait.
La pression reste constante
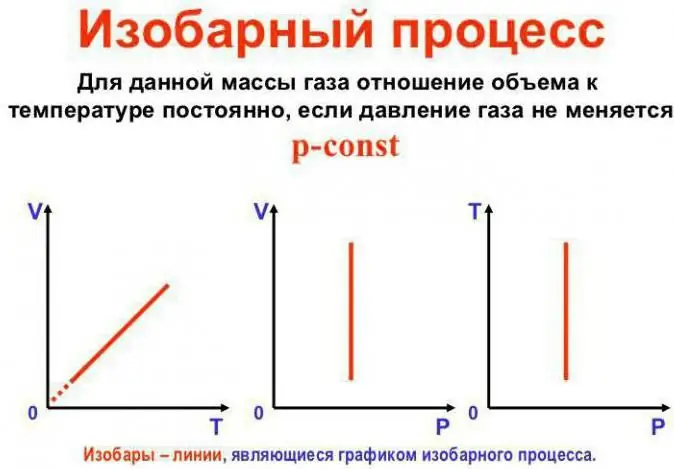
C'est la loi de Gay-Lussac. Il ressemble à ceci: V/T=const. Il peut être réécrit d'une autre manière: V=Vo (1 + at). Ici a est égal à 1/273,15 K^-1 et est appelé "coefficient d'expansion volumique". Nous pouvons substituer la température en degrés Celsius etl'échelle Kelvin. Dans ce dernier cas, on obtient la formule V=Voat.
Le volume reste constant

Il s'agit de la deuxième loi de Gay-Lussac, plus communément appelée loi de Charles. Il ressemble à ceci: p/T=const. Il existe une autre formulation: p=po (1 + at). Les transformations peuvent être réalisées conformément à l'exemple précédent. Comme vous pouvez le voir, les lois des gaz parfaits sont parfois assez similaires les unes aux autres.
La température reste constante

Si la température d'un gaz parfait reste constante, alors on peut obtenir la loi de Boyle-Mariotte. Il peut être écrit comme ceci: pV=const.
Concept associé 2: Pression partielle
Disons que nous avons un récipient avec des gaz. Ce sera un mélange. Le système est dans un état d'équilibre thermique et les gaz eux-mêmes ne réagissent pas les uns avec les autres. Ici N désignera le nombre total de molécules. N1, N2 et ainsi de suite, respectivement, le nombre de molécules dans chacun des composants du mélange. Prenons la formule de pression p=nkT=NkT/V. Il peut être ouvert pour un cas particulier. Pour un mélange à deux composants, la formule prendra la forme: p=(N1 + N2) kT/V. Mais ensuite, il s'avère que la pression totale sera additionnée des pressions partielles de chaque mélange. Ainsi, cela ressemblera à p1 + p2 et ainsi de suite. Ce seront les pressions partielles.
À quoi ça sert ?
La formule que nous avons obtenue indique que la pression dans le système provient de chaque groupe de molécules. D'ailleurs, cela ne dépend pas deautres. D alton en a profité pour formuler la loi, qui portera son nom plus tard: dans un mélange où les gaz ne réagissent pas chimiquement entre eux, la pression totale sera égale à la somme des pressions partielles.






