Les phénomènes et processus naturels qui nous entourent sont assez complexes. Pour leur description physique exacte, un appareil mathématique encombrant doit être utilisé et un grand nombre de facteurs significatifs doivent être pris en compte. Pour éviter ce problème, certains modèles simplifiés sont utilisés en physique, ce qui facilite grandement l'analyse mathématique du processus, mais n'affecte pratiquement pas la précision de sa description. L'un d'eux est le modèle des gaz parfaits. Examinons-le plus en détail dans l'article.
Le concept de gaz parfait
Un gaz parfait est un état d'agrégation d'une substance, qui se compose de points matériels qui n'interagissent pas les uns avec les autres. Expliquons cette définition plus en détail.
Premièrement, nous parlons de points matériels en tant qu'objets qui composent un gaz parfait. Cela signifie que ses molécules et ses atomes n'ont pas de taille, mais ont une certaine masse. C'est audacieuxune approximation peut être faite en tenant compte du fait que dans tous les gaz réels à basse pression et à haute température, la distance entre les molécules est bien supérieure à leurs dimensions linéaires.
Deuxièmement, les molécules d'un gaz parfait ne doivent pas interagir entre elles. En réalité, de telles interactions existent toujours. Ainsi, même les atomes de gaz nobles subissent une attraction dipôle-dipôle. En d'autres termes, les interactions de van der Waals sont présentes. Cependant, comparées à l'énergie cinétique de rotation et au mouvement de translation des molécules, ces interactions sont si faibles qu'elles n'affectent pas les propriétés des gaz. Par conséquent, ils ne peuvent pas être pris en compte lors de la résolution de problèmes pratiques.
Il est important de noter que tous les gaz dont la densité est faible et la température élevée ne peuvent pas être considérés comme idéaux. En plus des interactions de van der Waals, il existe d'autres types de liaisons plus fortes, par exemple les liaisons hydrogène entre les molécules H2O, qui conduisent à une violation flagrante des conditions d'idéalité du gaz. Pour cette raison, la vapeur d'eau n'est pas un gaz parfait, mais l'air l'est.
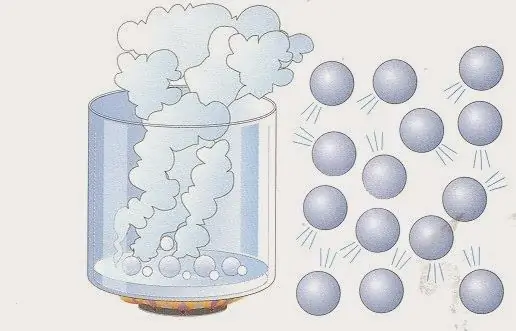
Modèle physique d'un gaz parfait
Ce modèle peut être représenté comme suit: supposons que le système gazeux contienne N particules. Ceux-ci peuvent être des atomes et des molécules de divers produits chimiques et éléments. Le nombre de particules N est grand, donc l'unité "mole" est généralement utilisée pour le décrire (1 mole correspond au nombre d'Avogadro). Ils se déplacent tous dans un certain volume V. Mouvements de particulessont chaotiques et indépendants les uns des autres. Chacun d'eux a une certaine vitesse v et se déplace le long d'une trajectoire rectiligne.
Théoriquement, la probabilité de collision entre particules est quasi nulle, puisque leur taille est petite par rapport aux distances interparticulaires. Cependant, si une telle collision se produit, elle est alors absolument élastique. Dans ce dernier cas, la quantité de mouvement totale des particules et leur énergie cinétique sont conservées.
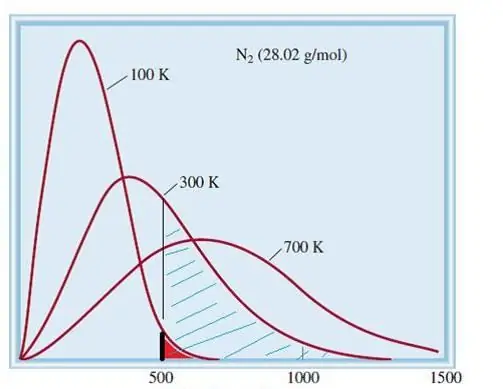
Le modèle considéré des gaz parfaits est un système classique avec un grand nombre d'éléments. Par conséquent, la vitesse et l'énergie des particules qu'il contient obéissent à la distribution statistique de Maxwell-Boltzmann. Certaines particules ont des vitesses faibles, tandis que d'autres ont des vitesses élevées. Dans ce cas, il existe une certaine limite de vitesse étroite, dans laquelle se trouvent les valeurs les plus probables de cette quantité. La distribution de vitesse des molécules d'azote est illustrée schématiquement ci-dessous.
Théorie cinétique des gaz
Le modèle des gaz parfaits décrit ci-dessus détermine de manière unique les propriétés des gaz. Ce modèle a été proposé pour la première fois par Daniel Bernoulli en 1738.

Par la suite, il a été développé jusqu'à son état actuel par August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski et d'autres scientifiques.
La théorie cinétique des substances fluides, sur la base de laquelle est construit le modèle des gaz parfaits, explique deux propriétés macroscopiques importantes du système en fonction de son comportement microscopique:
- La pression dans les gaz est le résultat de la collision de particules avec les parois du récipient.
- La température dans le système est le résultat de la manifestation du mouvement constant des molécules et des atomes.
Développons les deux conclusions de la théorie cinétique.
Pression de gaz
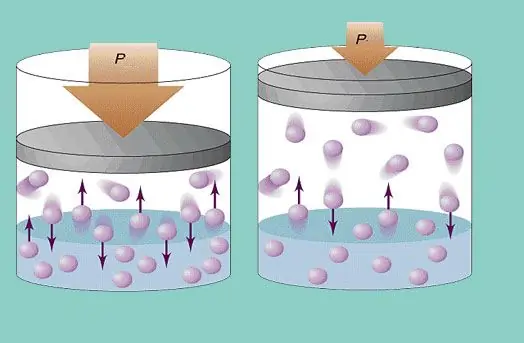
Le modèle des gaz parfaits suppose un mouvement chaotique constant des particules dans le système et leur collision constante avec les parois de la cuve. Chacune de ces collisions est considérée comme absolument élastique. La masse des particules est faible (≈10-27-10-25 kg). Par conséquent, il ne peut pas créer beaucoup de pression lors d'une collision. Néanmoins, le nombre de particules, et donc le nombre de collisions, est énorme (≈1023). De plus, la vitesse quadratique moyenne des éléments est de plusieurs centaines de mètres par seconde à température ambiante. Tout ceci conduit à la création d'une pression appréciable sur les parois de la cuve. Il peut être calculé à l'aide de la formule suivante:
P=Nmvcp2 / (3V), où vcp est la vitesse quadratique moyenne, m est la masse des particules.
Température absolue
Selon le modèle des gaz parfaits, la température est uniquement déterminée par l'énergie cinétique moyenne d'une molécule ou d'un atome dans le système étudié. Vous pouvez écrire l'expression suivante qui relie l'énergie cinétique et la température absolue pour un gaz parfait:
mvcp2 / 2=3 / 2kB T.
Ici kB est la constante de Boltzmann. De cette égalité on obtient:
T=m vcp2 / (3kB).
Équation d'état universelle
Si nous combinons les expressions ci-dessus pour la pression absolue P et la température absolue T, nous pouvons écrire l'égalité suivante:
PV=nRT.
Ici n est la quantité de substance en moles, R est la constante des gaz introduite par D. I. Mendeleïev. Cette expression est l'équation la plus importante de la théorie des gaz parfaits, car elle combine trois paramètres thermodynamiques (V, P, T) et ne dépend pas des caractéristiques chimiques du système gazeux.

L'équation universelle a d'abord été dérivée expérimentalement par le physicien français Emile Clapeyron au 19ème siècle, puis amenée à sa forme moderne par le chimiste russe Mendeleïev, c'est pourquoi elle porte actuellement les noms de ces scientifiques.






