L'un des sujets les plus difficiles et les plus incompréhensibles des mathématiques universitaires est l'intégration et le calcul différentiel. Vous devez connaître et comprendre ces concepts, ainsi que savoir les appliquer. De nombreuses disciplines techniques universitaires sont liées aux différentiels et aux intégrales.
Brèves informations sur les équations
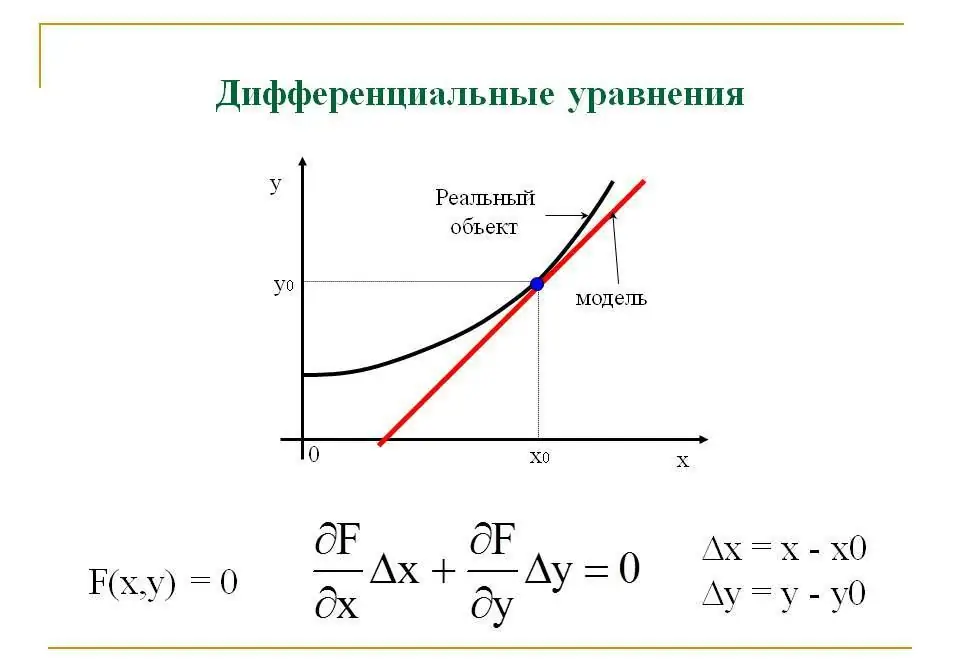
Ces équations sont l'un des concepts mathématiques les plus importants du système éducatif. Une équation différentielle est une équation qui relie les variables indépendantes, la fonction à trouver et les dérivées de cette fonction aux variables supposées indépendantes. Le calcul différentiel pour trouver une fonction d'une variable est appelé ordinaire. Si la fonction recherchée dépend de plusieurs variables, on parle alors d'une équation aux dérivées partielles.
En fait, trouver une certaine réponse à l'équation revient à l'intégrer, et la méthode de résolution est déterminée par le type d'équation.
Équations du premier ordre

Une équation différentielle du premier ordre est une équation qui peut décrire une variable, une fonction souhaitée et sa première dérivée. De telles équations peuvent être données sous trois formes: explicite, implicite, différentielle.
Concepts nécessaires pour résoudre
Condition initiale - définition de la valeur de la fonction souhaitée pour une valeur donnée d'une variable indépendante.
Solution d'une équation différentielle - toute fonction différentiable, exactement substituée dans l'équation d'origine, la transforme en identiquement égale. La solution obtenue, qui n'est pas explicite, est l'intégrale de l'équation.
La solution générale des équations différentielles est une fonction y=y(x;C), qui peut satisfaire les jugements suivants:
- Une fonction ne peut avoir qu'une seule constante arbitraire С.
- La fonction résultante doit être une solution à l'équation pour toutes les valeurs arbitraires d'une constante arbitraire.
- Avec une condition initiale donnée, une constante arbitraire peut être définie de manière unique afin que la solution particulière résultante soit cohérente avec la condition initiale initiale donnée.
En pratique, le problème de Cauchy est souvent utilisé - trouver une solution qui est particulière et peut être comparée à la condition définie au début.
Le théorème de Cauchy est un théorème qui met l'accent sur l'existence et l'unicité d'une solution particulière en calcul différentiel.
Sens géométrique:
- Solution générale y=y(x;C)l'équation est le nombre total de courbes intégrales.
- Le calcul différentiel vous permet de relier les coordonnées d'un point dans le plan XOY et la tangente tracée à la courbe intégrale.
- Définir la condition initiale signifie définir un point sur le plan.
- Résoudre le problème de Cauchy signifie que parmi l'ensemble des courbes intégrales représentant la même solution de l'équation, il faut sélectionner la seule passant par le seul point possible.
- La satisfaction des conditions du théorème de Cauchy en un point signifie qu'une courbe intégrale (d'ailleurs une seule) passe nécessairement par le point choisi dans le plan.
Équation à variable séparable
Par définition, une équation différentielle est une équation où son côté droit décrit ou se reflète comme un produit (parfois un rapport) de deux fonctions, l'une dépendant uniquement de "x", et l'autre - uniquement de "y ". Un exemple clair pour ce genre: y'=f1(x)f2(y).
Pour résoudre des équations d'une forme particulière, il faut d'abord transformer la dérivée y'=dy/dx. Ensuite, en manipulant l'équation, vous devez l'amener à une forme où vous pouvez intégrer les deux parties de l'équation. Après les transformations nécessaires, nous intégrons les deux parties et simplifions le résultat.

Équations homogènes
Par définition, une équation différentielle peut être dite homogène si elle a la forme suivante: y'=g(y/x).
Dans ce cas, le remplacement y/x=est le plus souvent utilisét(x).
Pour résoudre de telles équations, il est nécessaire de réduire une équation homogène à une forme à variables séparables. Pour ce faire, vous devez effectuer les opérations suivantes:
- Affiche, exprimant la dérivée de la fonction originale, à partir de n'importe quelle fonction originale comme une nouvelle équation.
- L'étape suivante consiste à transformer la fonction résultante sous la forme f(x;y)=g(y/x). En termes plus simples, faites en sorte que l'équation ne contienne que le rapport y/x et des constantes.
- Faites le remplacement suivant: y/x=t(x); y=t(x)x; y'=t'x + t. La substitution effectuée aidera à diviser les variables de l'équation, en la ramenant progressivement à une forme plus simple.
Équations linéaires
La définition de ces équations est la suivante: une équation différentielle linéaire est une équation où son côté droit est exprimé sous la forme d'une expression linéaire par rapport à la fonction d'origine. La fonction souhaitée dans ce cas: y'=a(x)y + b(x).
Reformons la définition comme suit: toute équation du 1er ordre deviendra linéaire dans sa forme si la fonction d'origine et sa dérivée sont incluses dans l'équation du premier degré et ne sont pas multipliées l'une par l'autre. La "forme classique" d'une équation différentielle linéaire a la structure suivante: y' + P(x)y=Q(x).
Avant de résoudre une telle équation, il convient de la convertir en "forme classique". La prochaine étape sera le choix de la méthode de résolution: la méthode de Bernoulli ou la méthode de Lagrange.
Résoudre l'équation avecen utilisant la méthode introduite par Bernoulli, implique la substitution et la réduction d'une équation différentielle linéaire à deux équations à variables distinctes relatives aux fonctions U(x) et V(x), qui ont été données dans leur forme originale.
La méthode de Lagrange consiste à trouver une solution générale à l'équation d'origine.
- Il faut trouver la même solution de l'équation homogène. Après recherche, nous avons la fonction y=y(x, C), où C est une constante arbitraire.
- Nous recherchons une solution à l'équation originale sous la même forme, mais nous considérons C=C(x). Nous substituons la fonction y=y(x, C(x)) dans l'équation d'origine, trouvons la fonction C(x) et écrivons la solution de l'équation générale d'origine.
Équation de Bernoulli
Équation de Bernoulli - si le côté droit du calcul prend la forme f(x;y)=a(x)y + b(x)yk, où k est toute valeur numérique rationnelle possible, ne prenant pas comme exemples de cas où k=0 et k=1.
Si k=1, alors le calcul devient séparable, et quand k=0, l'équation reste linéaire.
Considérons le cas général de la résolution de ce type d'équation. Nous avons l'équation standard de Bernoulli. Il doit être réduit à un linéaire, pour cela, vous devez diviser l'équation par yk. Après cette opération, remplacer z(x)=y1-k. Après une série de transformations, l'équation sera réduite à une équation linéaire, le plus souvent par la méthode de substitution z=UV.
Équations en différentiels totaux
Définition. Une équation de structure P(x;y)dx + Q(x;y)dy=0 est appelée une équation en toutes lettresdifférentielles, si la condition suivante est remplie (dans cette condition, "d" est une différentielle partielle): dP(x;y)/dy=dQ(x;y)/dx.
Toutes les équations différentielles du premier ordre considérées précédemment peuvent être affichées sous forme de différentielles.

De tels calculs sont résolus de plusieurs manières. Mais, cependant, ils commencent tous par une vérification de l'état. Si la condition est satisfaite, alors la région la plus à gauche de l'équation est la différentielle totale de la fonction encore inconnue U(x;y). Ensuite, conformément à l'équation, dU (x; y) sera égal à zéro, et donc la même intégrale de l'équation en différentiels totaux sera affichée sous la forme U (x; y) u003d C. Par conséquent, le solution de l'équation se réduit à trouver la fonction U (x; y).
Facteur d'intégration
Si la condition dP(x;y)/dy=dQ(x;y)/dx n'est pas satisfaite dans l'équation, alors l'équation n'a pas la forme que nous avons considérée ci-dessus. Mais parfois il est possible de choisir une fonction M(x;y), multipliée par laquelle l'équation prend la forme d'une équation en "diffurs" complet. La fonction M (x;y) est appelée facteur d'intégration.
Un intégrateur ne peut être trouvé que lorsqu'il devient une fonction d'une seule variable.






