En physique, le sujet de la connexion en parallèle et en série est étudié, et il peut s'agir non seulement de conducteurs, mais aussi de condensateurs. Il est important ici de ne pas se tromper sur l'apparence de chacun d'eux sur le diagramme. Et seulement ensuite appliquer des formules spécifiques. Au fait, vous devez vous en souvenir par cœur.
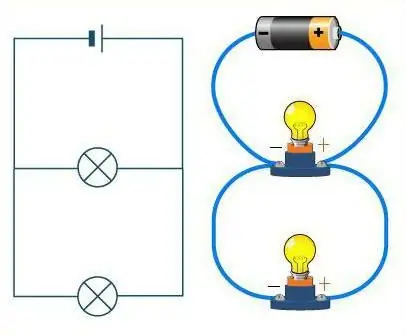
Comment distinguer ces deux composés ?
Regardez attentivement le schéma. Si les fils sont représentés comme une route, les voitures qui s'y trouvent joueront le rôle de résistances. Sur une route droite sans fourches, les voitures roulent les unes après les autres, en chaîne. La connexion en série des conducteurs a également la même apparence. La route dans ce cas peut avoir un nombre illimité de virages, mais pas une seule intersection. Peu importe comment la route (câbles) remua, les machines (résistances) seront toujours situées les unes après les autres, dans une chaîne.
C'est une tout autre affaire si une connexion parallèle est envisagée. Ensuite, les résistances peuvent être comparées aux athlètes au départ. Ils sontchacun se tient sur sa propre piste, mais ils ont le même sens de déplacement, et la ligne d'arrivée est au même endroit. De même, les résistances - chacune d'elles a son propre fil, mais elles sont toutes connectées à un moment donné.
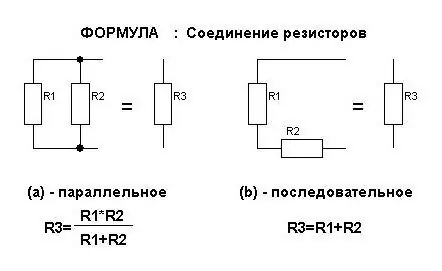
Formules pour la force actuelle
Il est toujours discuté dans le sujet "Électricité". Les connexions parallèles et en série affectent la quantité de courant dans les résistances de différentes manières. Pour eux, des formules sont dérivées qui peuvent être mémorisées. Mais il suffit juste de se souvenir du sens qui leur est investi.
Donc, le courant dans la connexion en série des conducteurs est toujours le même. Autrement dit, dans chacun d'eux, la valeur de la force actuelle n'est pas différente. Vous pouvez faire une analogie si vous comparez un fil avec un tuyau. L'eau y coule toujours de la même manière. Et tous les obstacles sur son chemin seront balayés avec la même force. Idem avec le courant. Par conséquent, la formule du courant total dans un circuit avec une connexion en série de résistances ressemble à ceci:
I gen=I 1=I 2
Ici, la lettre I dénote la force du courant. Il s'agit d'une notation courante, vous devez donc vous en souvenir.
Le courant en parallèle ne sera plus une valeur constante. Avec la même analogie avec un tuyau, il s'avère que l'eau sera divisée en deux flux si le tuyau principal a une branche. Le même phénomène est observé avec le courant lorsqu'une ramification de fils apparaît sur son trajet. La formule de l'intensité totale du courant lorsque les conducteurs sont connectés en parallèle:
I gen=I 1 + I 2
Si la dérivation est composée de fils quiplus de deux, alors dans la formule ci-dessus, il y aura plus de termes du même nombre.
Formules pour le stress
Lorsqu'on considère un circuit dans lequel les conducteurs sont connectés en série, la tension dans toute la section est déterminée par la somme de ces valeurs sur chaque résistance spécifique. Vous pouvez comparer cette situation avec des assiettes. Il sera facile pour une personne d'en tenir une, il pourra aussi prendre la seconde à proximité, mais avec difficulté. Une personne ne pourra plus tenir trois assiettes côte à côte, l'aide d'une seconde sera nécessaire. Etc. Les efforts des gens s'additionnent.
La formule de la tension totale d'une section d'un circuit avec une connexion en série de conducteurs ressemble à ceci:
U gen=U 1 + U 2, où U est la désignation adoptée pour la tension électrique.
Une autre situation se présente si une connexion parallèle de résistances est envisagée. Lorsque les assiettes sont empilées les unes sur les autres, elles peuvent toujours être tenues par une seule personne. Vous n'avez donc rien à ajouter. La même analogie est observée lorsque les conducteurs sont connectés en parallèle. La tension sur chacun d'eux est la même et égale à celle qui est sur tous à la fois. La formule pour la tension totale est:
U gen=U 1=U 2
Formules de résistance électrique
Vous ne pouvez plus les mémoriser, mais connaître la formule de la loi d'Ohm et en déduire celle que vous souhaitez. Il résulte de cette loi quela tension est égale au produit du courant et de la résistance. Autrement dit, U=IR, où R est la résistance.
Ensuite, la formule avec laquelle vous devrez travailler dépend de la manière dont les conducteurs sont connectés:
- en série, vous avez donc besoin d'une tension égale - IgenRtotal=I1R1 + I2R2;
- en parallèle, il faut utiliser la formule de l'intensité du courant - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Suivi de transformations simples, qui sont basées sur le fait que dans la première égalité tous les courants ont la même valeur, et dans la seconde - les tensions sont égales. Ils peuvent donc être raccourcis. Autrement dit, les expressions suivantes sont obtenues:
- R gen=R 1 + R 2 (pour la connexion en série des conducteurs).
- 1 / R gen=1 / R 1 + 1 / R 2(lorsqu'il est connecté en parallèle).
Lorsque le nombre de résistances connectées au réseau augmente, le nombre de termes dans ces expressions change.
Il convient de noter que la connexion en parallèle et en série des conducteurs a un effet différent sur la résistance totale. Le premier d'entre eux réduit la résistance de la section de circuit. De plus, elle s'avère inférieure à la plus petite des résistances utilisées. Lorsqu'il est connecté en série, tout est logique: les valeurs s'additionnent, donc le nombre total sera toujours le plus grand.
Travail en cours
Les trois grandeurs précédentes constituent les lois de la connexion en parallèle et de la disposition en série des conducteurs dans un circuit. Il est donc impératif de les connaître. À propos de travail et de puissance, il vous suffit de vous rappeler la formule de base. Il s'écrit comme suit: A \u003d IUt, où A est le travail du courant, t est le temps de son passage dans le conducteur.
Afin de déterminer le travail total avec une connexion série, vous devez remplacer la tension dans l'expression d'origine. Vous obtenez l'égalité: A \u003d I(U 1 + U 2)t, en ouvrant les parenthèses dans lesquelles il s'avère que le le travail sur l'ensemble de la section est égal à leur montant sur chaque consommateur actuel spécifique.
Le raisonnement se déroule de manière similaire si un schéma de connexion parallèle est considéré. Seule la force actuelle est censée être remplacée. Mais le résultat sera le même: A=A 1 + A 2.
Puissance actuelle
Lors de la dérivation d'une formule de puissance (notation "P") d'une section de circuit, vous devez à nouveau utiliser une formule: P \u003d UI. Après un tel raisonnement, il s'avère que les connexions parallèles et en série sont décrit par une telle formule de puissance: P \u003d P1 + P 2.
C'est-à-dire que, quelle que soit la manière dont les schémas sont élaborés, la puissance totale sera la somme des personnes impliquées dans le travail. Cela explique le fait qu'il est impossible d'inclure simultanément de nombreux appareils puissants dans le réseau de l'appartement. Elle ne peut tout simplement pas supporter la charge.
Comment la connexion des conducteurs affecte-t-elle la réparation de la guirlande du Nouvel An ?
Immédiatement après l'extinction de l'une des ampoules, il devient clair comment elles étaient connectées. Àconnexion série, aucun d'entre eux ne s'allumera. Cela est dû au fait qu'une lampe devenue inutilisable crée une coupure dans le circuit. Par conséquent, vous devez tout vérifier pour déterminer lequel est grillé, le remplacer - et la guirlande commencera à fonctionner.
S'il utilise une connexion parallèle, il ne s'arrête pas de fonctionner si l'une des ampoules tombe en panne. Après tout, la chaîne ne sera pas complètement rompue, mais seulement une partie parallèle. Pour réparer une telle guirlande, vous n'avez pas besoin de vérifier tous les éléments du circuit, mais seulement ceux qui ne brillent pas.
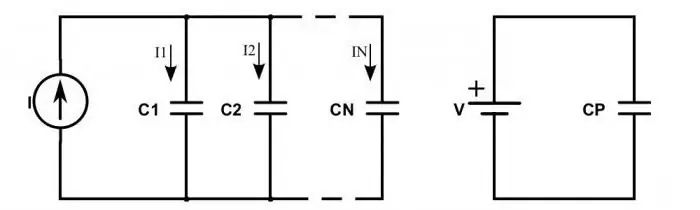
Qu'arrive-t-il à un circuit si des condensateurs sont inclus à la place des résistances ?
Lorsqu'ils sont connectés en série, la situation suivante est observée: les charges des plus de la source d'alimentation ne parviennent qu'aux plaques extérieures des condensateurs extrêmes. Ceux qui se trouvent entre les deux transmettent simplement cette charge le long de la chaîne. Ceci explique le fait que les mêmes charges apparaissent sur toutes les plaques, mais avec des signes différents. Par conséquent, la charge électrique de chaque condensateur connecté en série peut s'écrire comme suit:
q gen =q 1=q 2.
Afin de déterminer la tension sur chaque condensateur, vous aurez besoin de connaître la formule: U=q / C. Dans celle-ci, C est la capacité du condensateur.
La tension totale suit la même loi que les résistances. Par conséquent, en remplaçant la tension dans la formule de capacité par la somme, nous obtenons que la capacité totale des appareils doit être calculée à l'aide de la formule:
C=q / (U 1 + U2).
Vous pouvez simplifier cette formule en inversant les fractions et en remplaçant le rapport tension/charge par la capacité. Il s'avère l'égalité suivante: 1 / С=1 / С 1 + 1 / С 2.
La situation est quelque peu différente lorsque les condensateurs sont connectés en parallèle. Ensuite, la charge totale est déterminée par la somme de toutes les charges qui s'accumulent sur les plaques de tous les appareils. Et la valeur de la tension est toujours déterminée selon les lois générales. Par conséquent, la formule de la capacité totale des condensateurs connectés en parallèle est:
С=(q 1 + q 2) / U.
C'est-à-dire que cette valeur est considérée comme la somme de chacun des appareils utilisés dans la connexion:
S=S 1 + S 2.
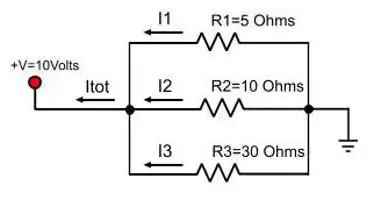
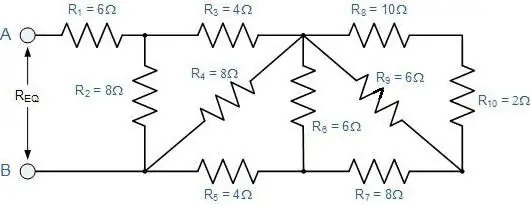
Comment déterminer la résistance totale d'une connexion arbitraire de conducteurs ?
C'est-à-dire une section dans laquelle des sections successives remplacent des sections parallèles, et vice versa. Pour eux, toutes les lois décrites sont toujours valables. Il vous suffit de les appliquer par étapes.
Premièrement, il est censé développer mentalement le schéma. S'il est difficile de l'imaginer, vous devez dessiner ce qui se passe. L'explication deviendra plus claire si nous la considérons avec un exemple spécifique (voir figure).
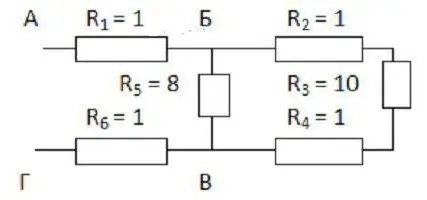
Il est pratique de commencer à dessiner à partir des points B et C. Ils doivent être placés à une certaine distance l'un de l'autre et des bords de la feuille. A gauche, un fil s'approche du point B, et deux sont déjà dirigés vers la droite. Le point B, en revanche, a deux branches sur la gauche et un fil après.
Maintenant, vous devez remplir l'espace entre cespoints. Trois résistances avec des coefficients de 2, 3 et 4 doivent être placées le long du fil supérieur, et celle avec un indice de 5 partira du bas. Les trois premières sont connectées en série. Avec la cinquième résistance, ils sont en parallèle.
Les deux résistances restantes (la première et la sixième) sont connectées en série avec la section considérée du BV. Ainsi, le dessin peut simplement être complété par deux rectangles de part et d'autre des points sélectionnés. Il reste à appliquer les formules de calcul de la résistance:
- première celle donnée pour la connexion série;
- then pour parallèle;
- et encore pour consécutifs.
De cette façon, vous pouvez déployer n'importe quel schéma, même très complexe.
Le problème de la connexion en série des conducteurs
État. Deux lampes et une résistance sont connectées dans un circuit l'une derrière l'autre. La tension totale est de 110 V et le courant est de 12 A. Quelle est la valeur de la résistance si chaque lampe est évaluée à 40 V ?
Décision. Puisqu'une connexion en série est envisagée, les formules de ses lois sont connues. Il suffit de les appliquer correctement. Commencez par trouver la valeur de la tension aux bornes de la résistance. Pour ce faire, vous devez soustraire deux fois la tension d'une lampe du total. Il s'avère que 30 V.
Maintenant que deux quantités sont connues, U et I (la seconde d'entre elles est donnée dans la condition, puisque le courant total est égal au courant dans chaque consommateur en série), nous pouvons calculer la résistance de la résistance en utilisant Loi d'Ohm. Il s'avère que c'est 2,5 ohms.
Répondre. La résistance de la résistance est de 2,5 ohms.
Tâchepour le raccordement de condensateurs, en parallèle et en série
État. Il y a trois condensateurs avec des capacités de 20, 25 et 30 microfarads. Déterminez leur capacité totale lorsqu'ils sont connectés en série et en parallèle.
Décision. Il est plus facile de commencer avec une connexion parallèle. Dans cette situation, il suffit d'ajouter les trois valeurs. Ainsi, la capacité totale est de 75 uF.
Les calculs seront un peu plus compliqués lorsque ces condensateurs seront connectés en série. Après tout, vous devez d'abord trouver le rapport d'unité à chacune de ces capacités, puis les additionner les unes aux autres. Il s'avère que l'unité divisée par la capacité totale est de 37/300. Ensuite, la valeur souhaitée est d'environ 8 microfarads.
Répondre. La capacité totale en connexion série est de 8 uF, en parallèle - 75 uF.






