La thermodynamique de l'état d'agrégat gazeux de la matière est une branche importante de la physique qui étudie l'équilibre thermodynamique et les transitions quasi-statiques dans les systèmes. Le modèle principal sur lequel reposent les prédictions du comportement des systèmes est le modèle des gaz parfaits. Avec son utilisation, l'équation de Mendeleev-Clapeyron a été obtenue. Considérez-le dans l'article.
Gaz idéal
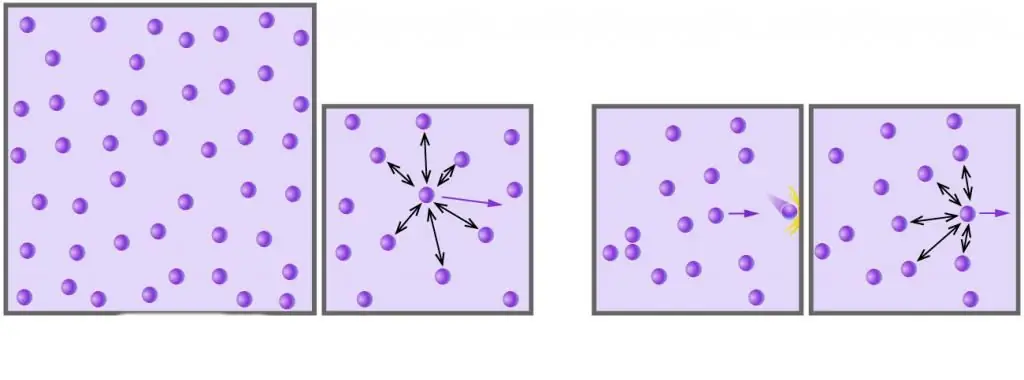
Comme vous le savez, tous les vrais gaz sont constitués de molécules ou d'atomes, dont les distances sont trop grandes par rapport à leur taille à basse pression. De plus, à haute température, à l'échelle absolue, l'énergie cinétique des molécules dépasse leur énergie potentielle associée à de faibles interactions dipôle-dipôle (si, en plus de ces interactions, il existe d'autres types de liaisons chimiques, par exemple ioniques ou l'hydrogène, alors ils apportent une contribution significative à la composante potentielle de l'énergie du système interne).
En raison dePour de nombreux gaz réels dans des conditions proches de la normale, on peut négliger leurs interactions internes et leurs tailles de particules. Ces deux principales approximations constituent le modèle des gaz parfaits.
Équation de Mendeleïev en physique

Il est plus correct et juste d'appeler cette équation la loi de Clapeyron-Mendeleïev. Le fait est qu'il a été enregistré pour la première fois par l'ingénieur français Emile Clapeyron en 1834. Il l'a fait en analysant les lois des gaz de Boyle-Mariotte, Gay-Lussac et Charles découvertes au début du 19ème siècle.
Le mérite du chimiste russe Dmitry Mendeleev réside dans le fait qu'il a donné à l'équation une forme mathématique moderne et facile à utiliser. En particulier, Mendeleïev a introduit dans l'équation une constante pour tous les gaz R=8, 314 J/(molK). Clapeyron lui-même a utilisé un certain nombre de constantes empiriques qui rendent le processus de calcul difficile.
L'équation de Mendeleïev-Clapeyron s'écrit comme suit:
PV=nRT.
Cette égalité signifie que le produit de la pression P et du volume V à gauche de l'expression est toujours proportionnel au produit de la température absolue T et de la quantité de substance n à gauche.
L'expression étudiée permet d'obtenir n'importe quelle loi des gaz si l'on fixe deux de ses quatre paramètres. Dans le cas des isoprocessus, on étudie des systèmes fermés dans lesquels il n'y a pas d'échange de matière avec le milieu (n=const). Ces processus sont caractérisés par un seul paramètre thermodynamique fixe (T, P ou V).

Exemple de problème
Résolvons maintenant le problème sur l'équation de Mendeleïev-Clapeyron. On sait que l'oxygène pesant 500 grammes se trouve dans une bouteille d'un volume de 100 litres à une pression de 2 atmosphères. Quelle est la température dans le ballon, sachant que le système est en équilibre thermodynamique.
Rappelons que, selon la définition, la quantité d'une substance est calculée par la formule:
n=m/M.
Où m est la masse de toutes les particules du système, M est leur masse molaire moyenne. Cette égalité permet de réécrire l'équation de Mendeleev sous la forme suivante:
PV=mRT/M.
Où nous obtenons la formule de travail pour cette tâche:
T=PVM/(mR).
Il reste à convertir toutes les quantités en unités SI et à les substituer dans cette expression:
T=21013250, 10, 032/(0, 58, 314)=156 K.
La température calculée est de -117 oC. Bien que l'oxygène à cette température soit encore gazeux (il se condense à -182,96 oC), dans de telles conditions le modèle de gaz parfait ne peut être utilisé que pour obtenir une estimation qualitative de la valeur calculée.






