En thermodynamique, lors de l'étude des transitions de l'état initial à l'état final d'un système, il est important de connaître l'effet thermique du processus. Le concept de capacité calorifique est étroitement lié à cet effet. Dans cet article, nous examinerons la question de savoir ce que l'on entend par la capacité calorifique isochore d'un gaz.
Gaz idéal
Un gaz parfait est un gaz dont les particules sont considérées comme des points matériels, c'est-à-dire qu'elles n'ont pas de dimensions, mais ont une masse, et dans lequel toute l'énergie interne consiste uniquement en l'énergie cinétique du mouvement des molécules et les atomes.
Tout gaz réel ne satisfera idéalement jamais le modèle décrit, puisque ses particules ont encore des dimensions linéaires et interagissent les unes avec les autres en utilisant des liaisons de van der Waals faibles ou des liaisons chimiques d'un autre type. Cependant, à basse pression et à haute température, les distances entre les molécules sont grandes et leur énergie cinétique dépasse l'énergie potentielle des dizaines de fois. Tout cela permet d'appliquer avec une grande précision le modèle idéal pour les gaz réels.
Énergie interne du gaz
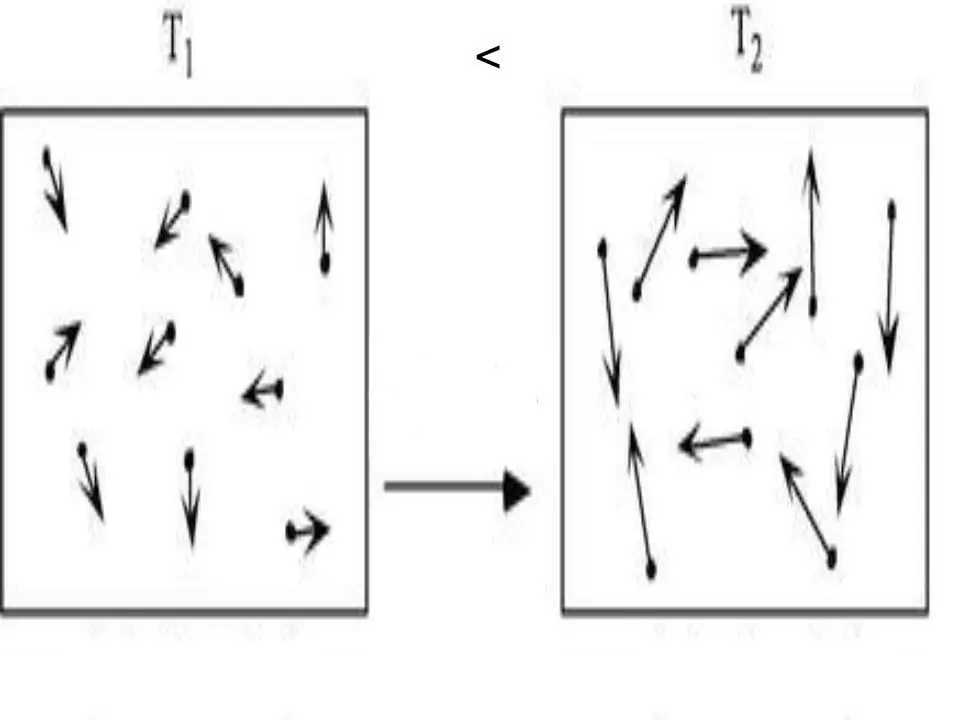
L'énergie interne de tout système est une caractéristique physique, qui est égale à la somme de l'énergie potentielle et cinétique. Puisque l'énergie potentielle peut être négligée dans les gaz parfaits, on peut écrire l'égalité pour eux:
U=Ek.
Où Ek est l'énergie du système cinétique. En utilisant la théorie de la cinétique moléculaire et en appliquant l'équation d'état universelle de Clapeyron-Mendeleev, il n'est pas difficile d'obtenir une expression pour U. Elle s'écrit ci-dessous:
U=z/2nRT.
Ici T, R et n sont respectivement la température absolue, la constante des gaz et la quantité de substance. La valeur z est un nombre entier indiquant le nombre de degrés de liberté d'une molécule de gaz.
Capacité calorifique isobare et isochore
En physique, la capacité calorifique est la quantité de chaleur qui doit être fournie au système étudié pour le chauffer d'un kelvin. La définition inverse est également vraie, c'est-à-dire que la capacité thermique est la quantité de chaleur que le système libère lorsqu'il est refroidi d'un kelvin.
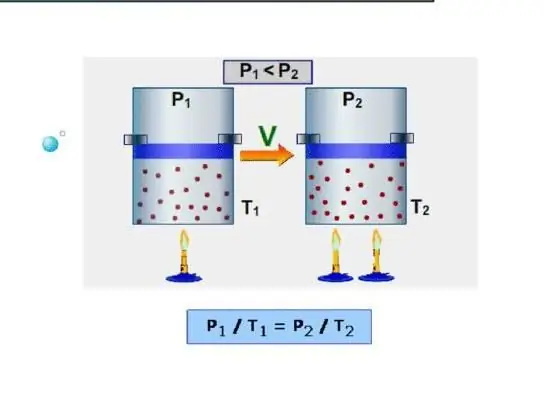
Le moyen le plus simple pour un système est de déterminer la capacité calorifique isochore. On l'entend comme la capacité calorifique à volume constant. Étant donné que le système n'effectue pas de travail dans de telles conditions, toute l'énergie est dépensée pour augmenter les réserves d'énergie internes. Désignons la capacité calorifique isochore par le symbole CV, alors on peut écrire:
dU=CVdT.
C'est-à-dire que le changement d'énergie internesystème est directement proportionnel à la variation de sa température. Si nous comparons cette expression avec l'égalité écrite dans le paragraphe précédent, alors nous arrivons à la formule pour CV dans un gaz parfait:
СV=z/2nR.
Cette valeur n'est pas pratique à utiliser car elle dépend de la quantité de substance dans le système. Par conséquent, le concept de capacité calorifique isochore spécifique a été introduit, c'est-à-dire une valeur calculée soit pour 1 mol de gaz, soit pour 1 kg. Notons la première valeur par le symbole CV, la seconde - par le symbole CV m. Pour eux, vous pouvez écrire les formules suivantes:
CV=z/2R;
CVm=z/2R/M.
Ici M est la masse molaire.
Isobarique est la capacité calorifique tout en maintenant une pression constante dans le système. Un exemple d'un tel processus est l'expansion du gaz dans un cylindre sous un piston lorsqu'il est chauffé. Contrairement au processus isochore, lors du processus isobare, la chaleur fournie au système est dépensée pour augmenter l'énergie interne et effectuer un travail mécanique, c'est-à-dire:
H=dU + PdV.
L'enthalpie d'un processus isobare est le produit de la capacité calorifique isobare et de la variation de température dans le système, c'est-à-dire:
H=CPdT.
Si l'on considère la détente à pression constante de 1 mole de gaz, alors la première loi de la thermodynamique s'écrira comme suit:
CPdT=CV dT + RdT.
Le dernier terme est obtenu à partir de l'équationClapeyron-Mendeleïev. De cette égalité découle la relation entre les capacités calorifiques isobare et isochore:
CP=CV + R.
Pour un gaz parfait, la capacité calorifique molaire spécifique à pression constante est toujours supérieure à la caractéristique isochore correspondante de R=8, 314 J/(molK).
Degrés de liberté des molécules et capacité calorifique
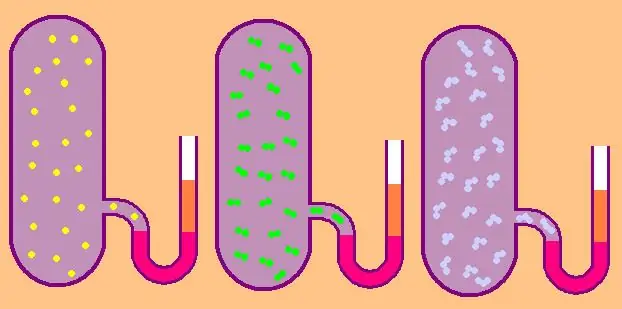
Écrivons à nouveau la formule de la capacité calorifique isochore molaire spécifique:
CV=z/2R.
Dans le cas d'un gaz monoatomique, la valeur z=3, puisque les atomes dans l'espace ne peuvent se déplacer que dans trois directions indépendantes.
Si nous parlons d'un gaz composé de molécules diatomiques, par exemple, l'oxygène O2 ou l'hydrogène H2, alors, en plus du mouvement de translation, ces molécules peuvent toujours tourner autour de deux axes mutuellement perpendiculaires, c'est-à-dire que z sera égal à 5.
Pour les molécules plus complexes, utilisez z=6. pour déterminer CV






