La réduction des fractions ordinaires est enseignée à l'école dans les cours de mathématiques. Si vous êtes un étudiant qui a manqué ce sujet en toute sécurité ou ne l'a pas compris, ou si vous êtes le parent d'un tel étudiant, alors ce sujet est fait pour vous. Comment réduire une fraction ? Facile et simple si vous suivez la méthode ci-dessous.
Qu'est-ce qu'une fraction commune
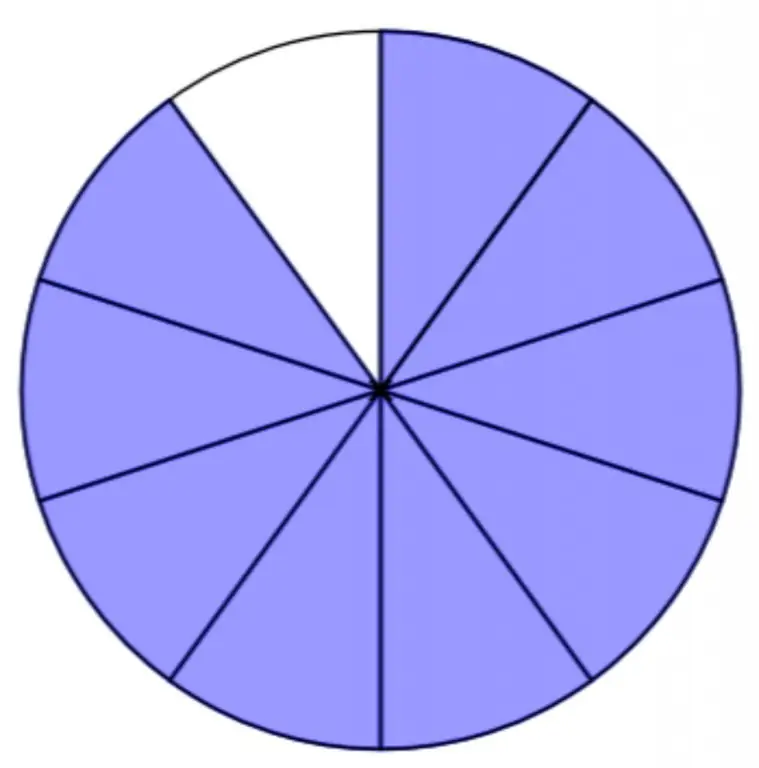
Rappelez-vous la théorie. Les fractions ordinaires apparaissent à la suite de la division d'un objet ou d'une unité de mesure en plusieurs parties égales. Prenons la tarte comme exemple. Si vous le coupez en dix parties et donnez ces dix parties à dix invités, alors dans une fraction ordinaire, cela ressemblera à 1/10 (un dixième). Mais sur la lettre, cela se reflétera dans une entrée à deux étages, dans laquelle un nombre au-dessus du tiret indique combien de pièces ont été prises, et en dessous du tiret se trouve leur nombre total.
Par exemple, la fraction 2/5 signifie qu'une personne n'a pris que deux parties sur cinq de quelque chose.
Passons à la question principale: comment réduire une fraction ?
Qu'est-ce que ça veut dire
Réduire une fraction signifie diviser le numérateur (le nombre au-dessus de la ligne) et le dénominateur (le nombre en dessous de la ligne) par le mêmele même nombre (il doit être supérieur à un). De plus, vous devez diviser jusqu'à ce que le numérateur et le dénominateur aient un nombre total par lequel ils pourraient être divisés.
Les fractions réduites sont des fractions qui ne peuvent pas être réduites davantage. Ils ne sont pas considérés comme réduits si le numérateur et le dénominateur ont toujours un nombre commun par lequel diviser chacun d'eux.
Abréviation
C'est réglé, passons à la question suivante. Regardons des exemples sur la façon de réduire une fraction.
Prenez la fraction 5/25. Par quel nombre divise-t-on ? Pour cinq. Réduisons-en le numérateur et le dénominateur. Le résultat est le nombre 1/5. Pouvez-vous couper plus loin ? Non.
Ou fraction 60/120. Par quel nombre peut-on les diviser ? Pour trente. Nous réduisons et obtenons le nombre 2/4. Pouvez-vous couper plus loin ? Oui, vous pouvez en couper deux autres. Obtenez 1/2.
Comment réduire la fraction "au nombre gagnant", c'est-à-dire ne pas la diviser plusieurs fois ? Essayez simplement de trouver le plus grand nombre qui divise le numérateur et le dénominateur. Lorsque nous avons analysé le deuxième exemple, la fraction 60/120, elle pouvait être divisée par soixante et obtenir immédiatement 1/2.
Si le plus grand nombre n'est pas immédiatement trouvé, essayez d'abord de diviser la fraction par n'importe quel nombre qui vous vient à l'esprit, puis essayez à nouveau de travailler avec la nouvelle fraction. L'essentiel est de réduire correctement et complètement la fraction. Peu importe le nombre de pas que vous faites pour y arriver, mais si vous appréciez votre temps, essayez de tout faire en une seule étape.






