L'algèbre propositionnelle est une science exacte qui ne fait aucun compromis. Pour résoudre des exemples avec conjonction, disjonction, implication, etc., vous pouvez créer une table de vérité dans l'application Excel. Il est équipé d'un ensemble de fonctions logiques qui automatisent et facilitent le processus de recherche du résultat.
Logique mathématique: concepts de base
Aristote est considéré comme le fondateur de la logique formelle. Au 17ème siècle G. Leibniz propose d'introduire des symboles pour définir les énoncés. D. Buhl a consolidé les connaissances acquises et a marqué pour la première fois les phrases avec des symboles.
Schématiquement, "TRUE" est remplacé par 1, et "FALSE" par 0.
Sous l'énoncé s'entend toute phrase déclarative qui donne une quelconque information et est susceptible de prendre valeur de vrai ou de faux. En algèbre, les logiques sont abstraites de la charge sémantique des phrases et ne considèrent que les valeurs logiques.
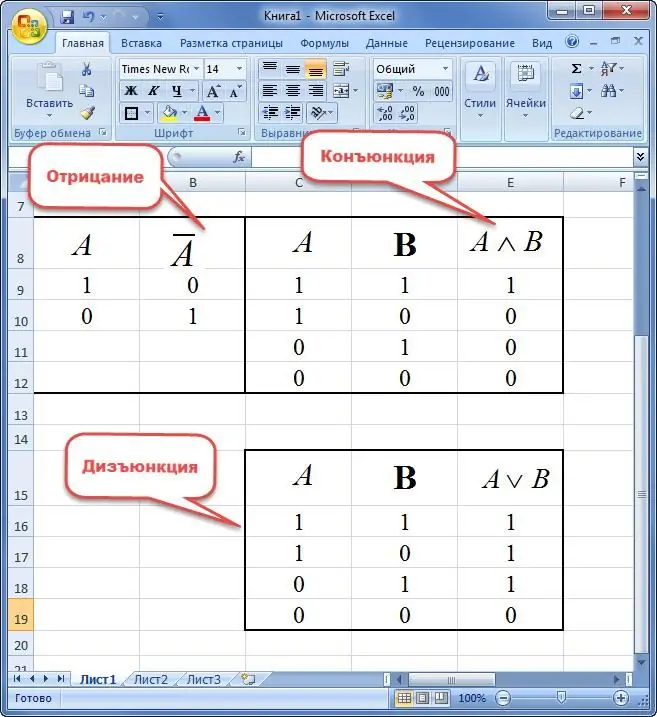
La négation est une nouvelle expression qui prend la valeur true si elle est fausse et vice versa.
Conjonction de deuxvariables est appelée une nouvelle phrase, qui prend la valeur de vérité en cas de désignation simultanée "1" et de fausseté dans les autres situations.
La disjonction de deux énoncés est comprise comme une nouvelle expression qui prend la valeur "FALSE" uniquement s'il y a "0" et "TRUE" dans d'autres variantes en même temps.
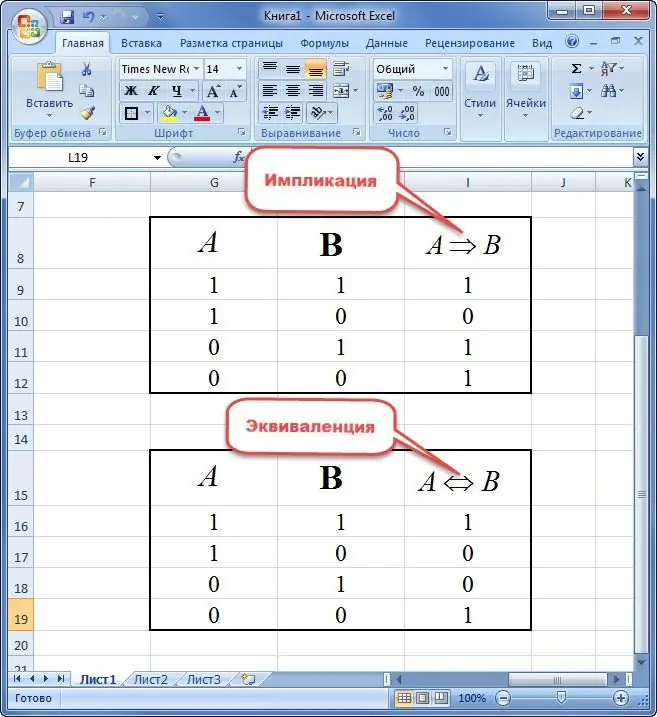
Une implication de deux variables est une nouvelle phrase dans laquelle:
- si la prémisse est vraie et la conséquence est fausse, alors l'expression vaut "0";
- instruction vaut "1" dans les autres cas.
Équivalent de deux variables est compris comme une nouvelle déclaration qui ne prend la valeur de vérité que si les éléments sont les mêmes. Sinon, l'offre est "0".
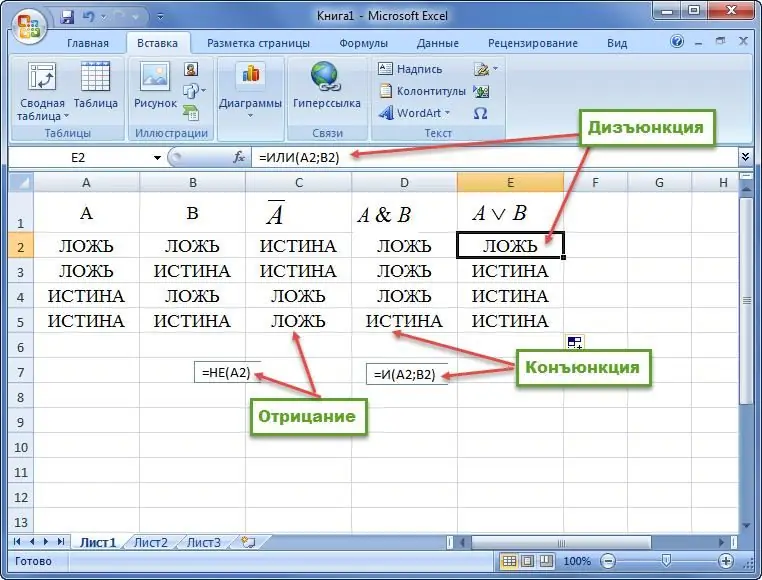
Les valeurs logiques des expressions sont généralement présentées sous forme de tableau. Il y a un autre nom pour ce genre d'information. Ils disent que pour une déclaration, vous devez construire une table de vérité. Il spécifie les valeurs initiales de toutes les variables, puis le résultat de l'expression entière est calculé.
Algorithme pour implémenter des calculs dans des opérations logiques
Pour construire une table de vérité, vous devez connaître l'ordre dans lequel les actions sont effectuées. Dans une expression à plusieurs opérandes, le calcul est effectué dans l'ordre suivant:
- inversion (négation);
- conjonction (fonction logique dans Excel "ET");
- disjonction (opérateur booléen dans Excel "OU");
- implication (conséquence);
- équivalence.
Il y a deux autres opérations, mais leur priorité n'est pas définie:
- coup de Schaeffer;
- Percer la flèche.
L'algorithme de calcul change si l'expression est entre parenthèses.
L'ordre de construction d'une forme tabulaire pour les opérandes logiques dans Excel
Avant de trouver la valeur d'une expression, vous devez étudier le concept d'une formule d'algèbre logique. La définition indique qu'il s'agit d'une expression complexe, constituée des déclarations les plus simples reliées par des opérandes logiques.
Exemple 1. Construisez une table de vérité pour la conjonction, la disjonction et la négation.
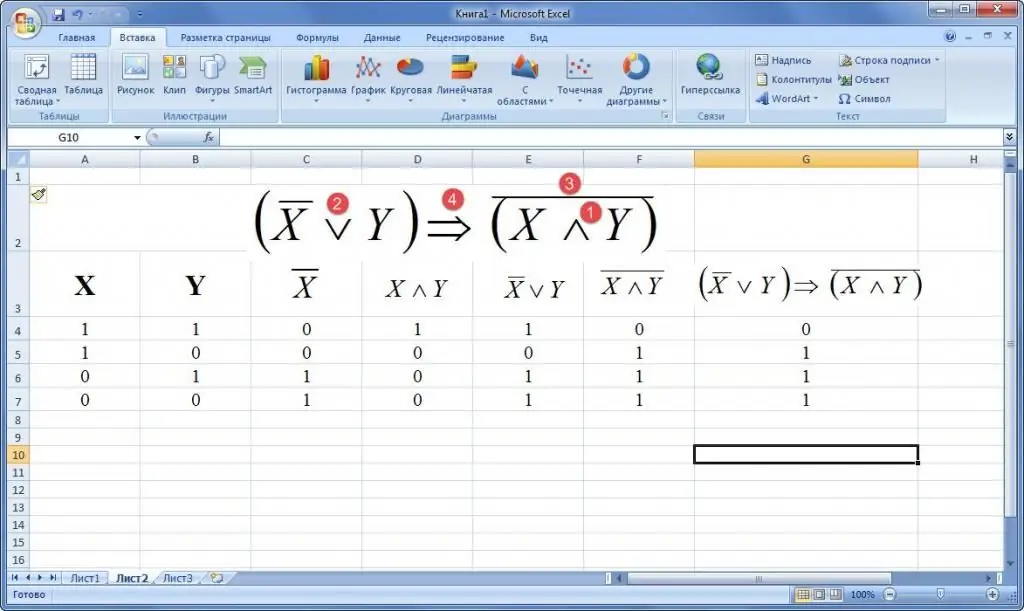
Exemple 2. Étant donné une formule pour l'algèbre de la logique. Construire une table de vérité. Des exemples d'exemples sont donnés ci-dessous.
Exemple 3. Comment construire une table de vérité dans Excel, étant donné une formule d'algèbre logique dans une description verbale. Dire: "Si un triangle est équilatéral, alors tous ses côtés sont égaux ou tous ses angles sont égaux."
D'abord, vous devez analyser la phrase composée en éléments minimaux:
- La première partie de l'expression: A="triangle équilatéral".
- Second: B="tous les côtés de la figure sont égaux".
- Troisième: C="tous les angles d'un triangle sont égaux".
Après cela, une expression est compilée et résolue dans le progiciel Excel.
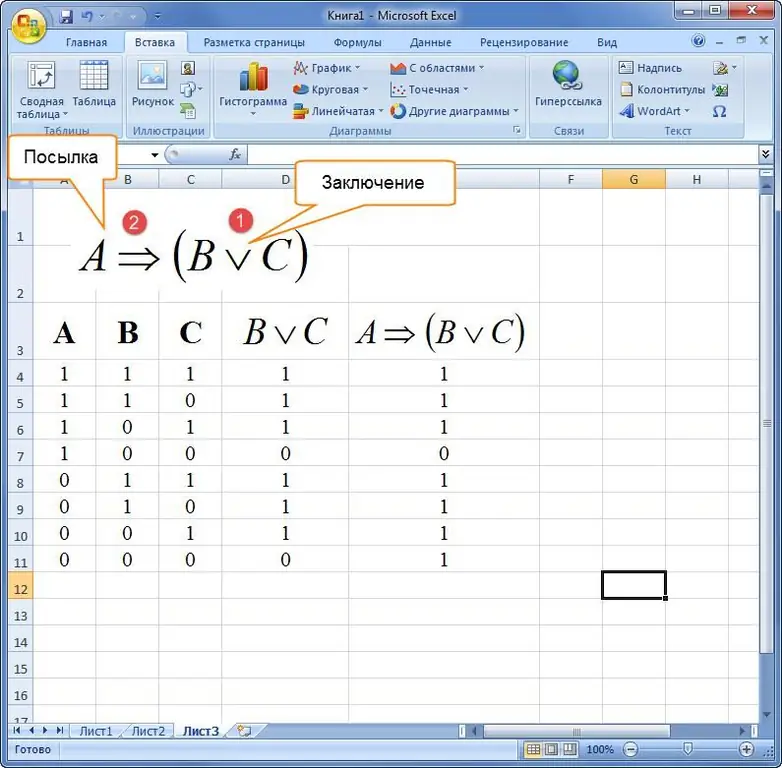
Lors de la compilation des tables de vérité, il est important de se souvenir de l'ordre des opérations.






