Une fonction linéaire est une ligne droite tracée le long d'une surface. Il peut être divisé en différents types et modèles. Ci-dessous, nous examinerons les formules pour l'obtenir, ainsi que pour atteindre sa perfection dans l'avion. Dans les dessins, vous pouvez pleinement vérifier cela et comprendre à quoi cela devrait ressembler.
Fonction linéaire y=kx + b
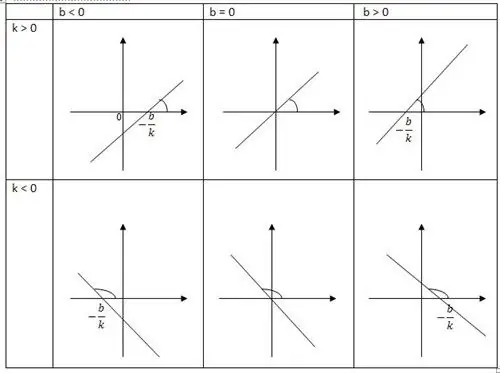
Cette valeur est une mesure précise d'une variable dans une vue. L'incrément fait référence à la propriété de base d'une fonction linéaire, il devient proportionnel à l'argument incrémenté. En d'autres termes, la fonction représente une généralisation de la proportionnalité directe. Une droite est le graphique d'une fonction linéaire. C'est de là que vient son nom. Une variable réelle touche une autre fonction réelle.
Propriétés
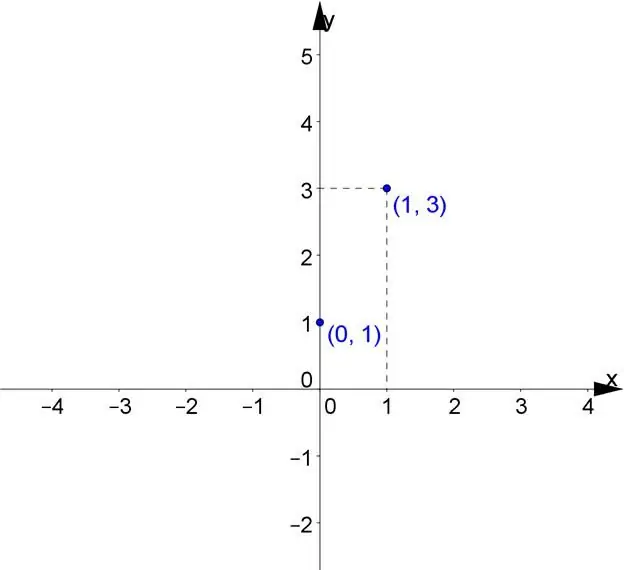
La fonction linéaire est une génératrice d'une ligne droite, qui a une direction positive de l'axe des x. L'un de ses facteurs de pente déterminants est k, il détermine la tangente de l'angle a. La droite formée dans la direction positive de l'axe des x est k. L'autre coordonnée b indiquecoordonnées du point, ainsi que l'intersection de la ligne avec l'axe.
Qu'est-ce qu'une fonction non linéaire ?
Les fonctions qui ne sont pas linéaires sont dites non linéaires. Il s'agit d'une relation mathématique entre des variables. Les non linéaires ne peuvent pas être exprimés comme y=ax + b. Ce terme est utilisé dans les moments où il est nécessaire d'étudier le cas général. Ce processus commence par les degrés inférieurs. Dans ce cas, des corrections quadratiques sont prises en compte. Une telle fonction a une courbure continue.
L'équation non linéaire considérée est arbitraire. Un exemple de fonction non linéaire est y=x2. Les termes "fonction linéaire" sont souvent utilisés, avec un raffinement et l'ajout de "homogène". Il peut être appliqué à une application linéaire exacte de X, qui est un espace vectoriel. Une fonction linéaire est tout le système comme elle.






