Lors de l'évaluation par les pairs, par exemple, l'évaluation de la compétitivité des produits, il est nécessaire, comme dans tout travail scientifique, de procéder à un traitement statistique des données. Ce dernier commence par déterminer la cohérence des avis d'experts, dont l'expression numérique est le coefficient de concordance.
Pourquoi avons-nous besoin d'une évaluation par consensus d'experts ?
Cette évaluation est nécessaire, tout d'abord, car les avis des experts peuvent être très différents sur les paramètres estimés. Dans un premier temps, l'évaluation est réalisée en hiérarchisant les indicateurs et en leur attribuant un certain coefficient de signification (poids). Un classement incohérent fait que ces coefficients ne sont pas statistiquement fiables. Les avis d'experts avec leur nombre requis (plus de 7-10) doivent être distribués conformément à la loi normale.
La notion de coefficient de concordance
Alors. La cohérence est la concordance. Le coefficient est une grandeur sans dimension montrant le rapport de la dispersion à la dispersion maximale dans le cas général. Généralisons ces concepts.
Le coefficient de concordance est un nombre de 0 à 1, montrant la cohérence des avis d'experts lorsqueclassement de certaines propriétés. Plus cette valeur est proche de 0, moins la cohérence est considérée. Si la valeur de ce coefficient est inférieure à 0,3, les avis des experts sont considérés comme incohérents. Lorsque la valeur du coefficient est comprise entre 0,3 et 0,7, la cohérence est considérée comme moyenne. Une valeur supérieure à 0,7 est considérée comme une cohérence élevée.
Cas d'utilisation
Lors de la réalisation de recherches statistiques, des situations peuvent survenir dans lesquelles un objet peut être caractérisé non pas par deux séquences, qui sont traitées statistiquement à l'aide du coefficient de concordance, mais par plusieurs séquences, qui sont donc classées par des experts ayant le même niveau de professionnalisme dans un certain domaine.
La cohérence du classement effectué par les experts doit être déterminée pour confirmer l'exactitude de l'hypothèse selon laquelle les experts font des mesures relativement précises, ce qui permet la formation de divers regroupements dans des groupes d'experts, qui sont largement déterminés par des facteurs humains, principalement tels que les différences de points de vue, les concepts, les différentes écoles scientifiques, la nature de l'activité professionnelle, etc.
Brève description de la méthode de classement. Ses avantages et ses inconvénients
Lors du classement, la méthode de classement est utilisée. Son essence réside dans le fait que chaque propriété de l'objet se voit attribuer son propre rang spécifique. Par ailleurs, à chaque expert inclus dans le groupe d'experts, ce rang est attribuéindépendamment, d'où la nécessité de traiter ces données afin d'identifier la cohérence des avis d'experts. Ce processus est effectué en calculant le coefficient de concordance.
Le principal avantage de la méthode de classement est sa facilité de mise en œuvre.
Les principaux inconvénients de la méthode sont:
- un petit nombre d'objets de classement, car lorsque leur nombre dépasse 15-20, il devient difficile d'attribuer des scores de classement objectifs;
- Basé sur l'utilisation de cette méthode, la question de la distance significative entre les objets étudiés reste ouverte.
Lorsque vous utilisez cette méthode, il faut tenir compte du fait que les notations sont basées sur une sorte de modèle probabiliste, elles doivent donc être appliquées avec prudence, compte tenu de la portée.
Coefficient de rang de concordance de Kendall
Utilisé pour déterminer la relation entre les caractéristiques quantitatives et qualitatives caractérisant des objets homogènes et classés selon le même principe.
Ce coefficient est déterminé par la formule:
t=2S/(n(n-1)), où
S - la somme des différences entre le nombre de séquences et le nombre d'inversions sur la deuxième caractéristique;
n - nombre d'observations.

Algorithme de calcul:
- Les valeurs x sont classées par ordre croissant ou décroissant.
- Les valeurs y sont disposées dans l'ordre dans lequel elles correspondent aux valeurs x.
- Pour chaque rang successif de y, déterminez combien de valeurs de rang supérieur le suivent. Ils sont additionnés et la mesure de correspondance des séquences de rangs en x et y est calculée.
- De même, le nombre de rangs de y avec des valeurs inférieures est calculé, ce qui s'additionne également.
- Ajoutez le nombre de rangs avec des valeurs supérieures et le nombre de rangs avec des valeurs inférieures, ce qui donne la valeur S.
Ce coefficient montre la relation entre deux variables et, dans la plupart des cas, il est appelé coefficient de corrélation de rang de Kendall. Une telle dépendance peut être représentée graphiquement.
Détermination du coefficient
Comment ça se fait ? Si le nombre de caractéristiques ou de facteurs classés dépasse 2, le coefficient de concordance est utilisé, qui est essentiellement une variante multiple de la corrélation de rang.
Soyez prudent. Le calcul du coefficient de concordance est basé sur le rapport de l'écart de la somme des carrés des rangs de la somme moyenne des carrés des rangs, multipliée par 12, au carré des experts, multiplié par la différence entre le cube du nombre d'objets et le nombre d'objets.
Algorithme de calcul
Afin de comprendre d'où vient le nombre 12 dans le numérateur de la formule de calcul, regardons l'algorithme de détermination.
Pour chaque ligne avec les rangs d'un certain expert, la somme des rangs est calculée, qui est une valeur aléatoire.
Le coefficient de concordance est généralement défini comme le rapport de l'estimation de la variance (D) à la valeur maximale de l'estimation de la variance(Dmax). Formulons successivement les définitions de ces quantités.
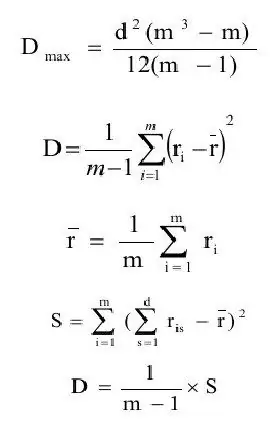
where ravg - estimation de l'attente;
m - nombre d'objets.
En remplaçant les formules résultantes par rapport à D par Dmax nous obtenons la formule finale pour le coefficient de concordance:
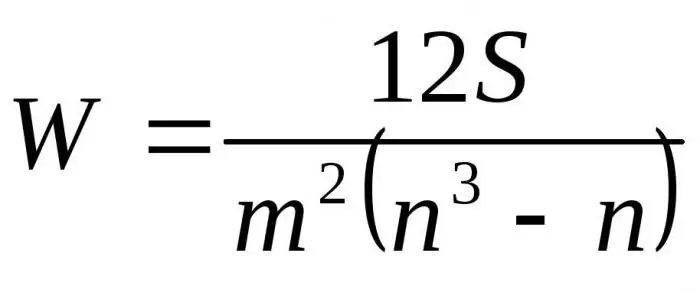
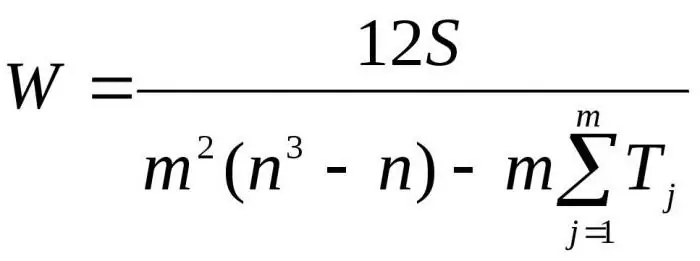
Ici m est le nombre d'experts, n est le nombre d'objets.
La première formule est utilisée pour déterminer le facteur de concordance s'il n'y a pas de rangs liés. La deuxième formule est utilisée s'il existe des rangs liés.
Donc, le calcul du coefficient de concordance est terminé. Et après? La valeur obtenue est évaluée pour la significativité à l'aide du coefficient de Pearson en multipliant ce coefficient par le nombre d'experts et par le nombre de degrés de liberté (m-1). Le critère résultant est comparé à la valeur du tableau, et si la valeur du premier dépasse la dernière, ils parlent de la signification du coefficient à l'étude.
Dans le cas de rangs liés, le calcul du critère de Pearson devient un peu plus compliqué et s'effectue par le rapport suivant: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Exemple
Supposons que la méthode experte évalue la compétitivité du beurre vendu dans un réseau de distribution. Donnons un exemple de calcul du coefficient de concordance. Avant d'évaluer la compétitivité, il est nécessaire de classer les consommateurspropriétés de ce produit qui sont impliquées dans l'évaluation. Supposons que ces propriétés seront les suivantes: goût et odeur, consistance et apparence, couleur, emballage et étiquetage, teneur en matière grasse, nom commercial, fabricant, prix.
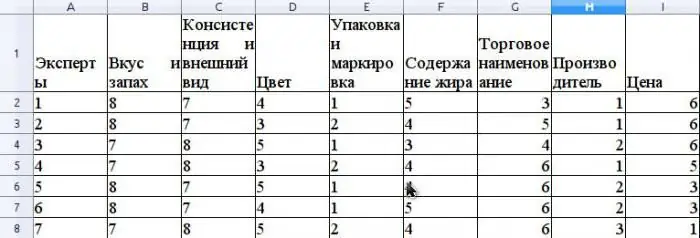
Supposons que le groupe d'experts se compose de 7 experts. La figure montre les résultats du classement de ces propriétés.
La valeur moyenne de r est calculée comme la moyenne arithmétique et sera de 31,5. Pour trouver S, additionnez les différences au carré entre ris et la moyenne de r, selon la formule ci-dessus, et déterminer que la valeur de S est 1718.
Calculez le coefficient de concordance en utilisant la formule sans utiliser les rangs liés (les rangs seraient liés si le même Expert Advisor avait les mêmes rangs pour différentes propriétés).
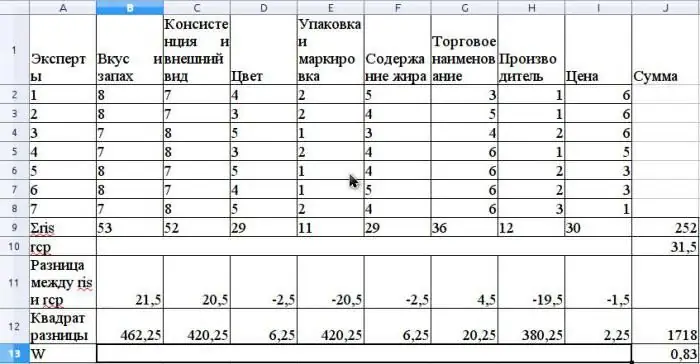
La valeur de ce coefficient sera de 0,83. Cela indique un fort consensus parmi les experts.
Vérifier sa signification à l'aide du test de Pearson:
7 x 0,83 x (8-1)=40,7.
Le test tabulaire de Pearson au seuil de signification de 1 % est de 18,5 et à 5 % - 14,1..
L'exemple démontre la simplicité et l'accessibilité du calcul pour toute personne connaissant les bases des calculs mathématiques. Pour les soulager,utiliser des feuilles de calcul.
En conclusion
Ainsi, le coefficient de concordance montre la cohérence des opinions de plusieurs experts. Plus il est éloigné de 0 et proche de 1, plus les avis sont cohérents. Ces coefficients doivent être confirmés par le calcul du critère de Pearson.






