La connaissance des définitions en physique est un facteur clé pour résoudre avec succès divers problèmes physiques. Dans cet article, nous examinerons ce que l'on entend par processus isobare, isochore, isotherme et adiabatique pour un système de gaz parfait.
Le gaz parfait et son équation
Avant de passer à la description des processus isobares, isochoriques et isothermes, considérons ce qu'est un gaz parfait. Selon cette définition en physique, ils considèrent un système composé d'un grand nombre de particules sans dimension et sans interaction qui se déplacent à grande vitesse dans toutes les directions. En fait, nous parlons d'un état d'agrégat gazeux de la matière, dans lequel les distances entre les atomes et les molécules dépassent de loin leurs tailles et dans lequel l'énergie potentielle d'interaction des particules est négligée en raison de sa petitesse, par rapport à l'énergie cinétique.
L'état d'un gaz parfait est l'ensemble de ses paramètres thermodynamiques. Les principaux sont la température, le volume et la pression. Désignons-les par les lettres T, V et P, respectivement. Dans les années 30 du XIXème siècleClapeyron (un scientifique français) a d'abord écrit une équation qui combine les paramètres thermodynamiques indiqués au sein d'une seule égalité. Il ressemble à:
PV=nRT,
où n et R sont respectivement la quantité de substances et la constante de gaz.
Que sont les isoprocessus dans les gaz ?
Comme beaucoup l'ont remarqué, les processus isobares, isochoriques et isothermes utilisent le même préfixe "iso" dans leurs noms. Cela signifie l'égalité d'un paramètre thermodynamique pendant le passage de l'ensemble du processus, tandis que les paramètres restants changent. Par exemple, un processus isotherme indique que, par conséquent, la température absolue du système est maintenue constante, tandis qu'un processus isochore indique un volume constant.
Les isoprocédés sont commodes à étudier, car la fixation d'un des paramètres thermodynamiques conduit à une simplification de l'équation générale de l'état des gaz. Il est important de noter que les lois des gaz pour tous ces isoprocessus ont été découvertes expérimentalement. Leur analyse a permis à Clapeyron d'obtenir l'équation universelle réduite.
Processus isobares, isochores et isothermes
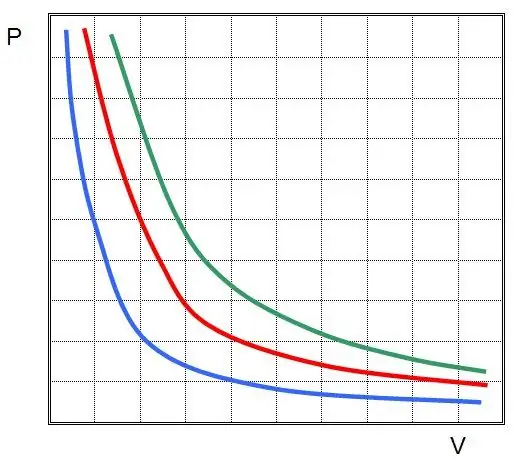
La première loi a été découverte pour un processus isotherme dans un gaz parfait. On l'appelle maintenant la loi Boyle-Mariotte. Puisque T ne change pas, l'équation d'état implique l'égalité:
PV=const.
En d'autres termes, tout changement de pression dans le système entraîne un changement inversement proportionnel de son volume, si la température du gaz est maintenue constante. Le graphique de la fonction P(V) esthyperbole.
Processus isobare - il s'agit d'un changement d'état du système, dans lequel la pression reste constante. Après avoir fixé la valeur de P dans l'équation de Clapeyron, on obtient la loi suivante:
V/T=const.
Cette égalité porte le nom du physicien français Jacques Charles, qui l'a reçue à la fin du XVIIIe siècle. L'isobare (représentation graphique de la fonction V(T)) ressemble à une ligne droite. Plus il y a de pression dans le système, plus vite cette ligne monte.
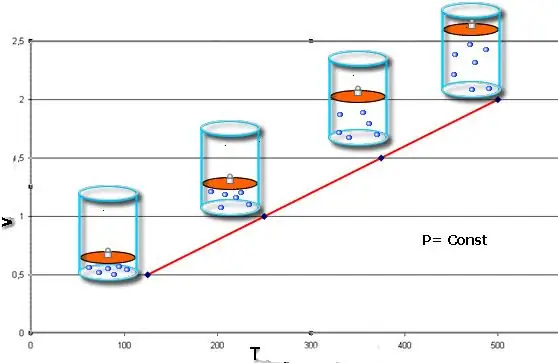
Le processus isobare est facile à mettre en œuvre si le gaz est chauffé sous le piston. Les molécules de ces derniers augmentent leur vitesse (énergie cinétique), créent une pression plus élevée sur le piston, ce qui entraîne la dilatation du gaz et maintient une valeur constante de P.
Enfin, le troisième isoprocessus est isochore. Il fonctionne avec un volume constant. De l'équation d'état, nous obtenons l'égalité correspondante:
P/T=const.
Elle est connue des physiciens sous le nom de loi de Gay-Lussac. La proportionnalité directe entre la pression et la température absolue indique que le graphique du processus isochore, comme le graphique de l'isobare, est une ligne droite avec une pente positive.
Il est important de comprendre que tous les isoprocessus se produisent dans des systèmes fermés, c'est-à-dire que la valeur de n est conservée pendant leur déroulement.
Processus adiabatique
Ce processus n'appartient pas à la catégorie "iso", puisque les trois paramètres thermodynamiques changent lors de son passage. adiabatiqueappelé la transition entre deux états du système, dans lequel il n'échange pas de chaleur avec l'environnement. Ainsi, l'expansion du système est réalisée grâce à ses réserves d'énergie internes, ce qui entraîne une baisse significative de la pression et de la température absolue.
Le processus adiabatique pour un gaz parfait est décrit par les équations de Poisson. L'un d'eux est illustré ci-dessous:
PVγ=const,
où γ est le rapport des capacités calorifiques à pression constante et à volume constant.
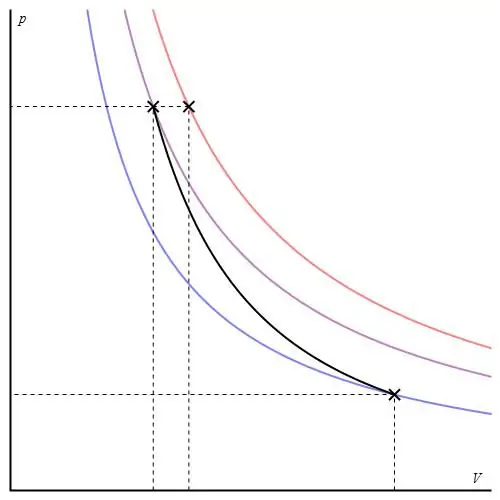
Le graphe adiabatique diffère du graphe de processus isochore et du graphe isobare, mais il s'apparente à une hyperbole (isotherme). L'adiabat dans les axes P-V se comporte plus brusquement que l'isotherme.






