Comme vous le savez, toute quantité physique appartient à l'un des deux types, elle est soit scalaire, soit vectorielle. Dans cet article, nous examinerons des caractéristiques cinématiques telles que la vitesse et l'accélération, et montrerons également où les vecteurs d'accélération et de vitesse sont dirigés.
Qu'est-ce que la vitesse et l'accélération ?
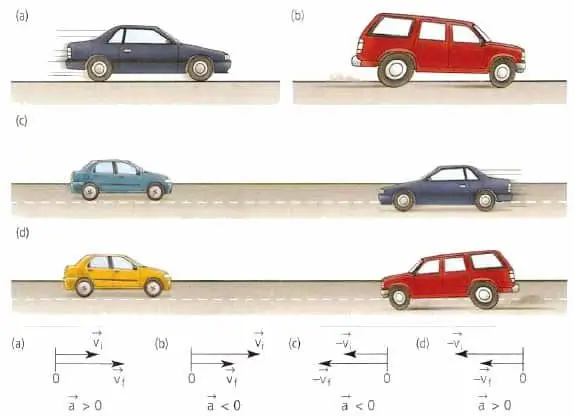
Les deux quantités mentionnées dans ce paragraphe sont des caractéristiques importantes de tout type de mouvement, qu'il s'agisse de déplacer un corps en ligne droite ou le long d'une trajectoire courbe.
La vitesse est la vitesse à laquelle les coordonnées changent dans le temps. Mathématiquement, cette valeur est égale à la dérivée temporelle de la distance parcourue, soit:
v¯=dl¯/dt.
Ici le vecteur l¯ est dirigé du point de départ du chemin vers le point final.
À son tour, l'accélération est la vitesse à laquelle la vitesse elle-même change dans le temps. Sous forme de formule, il peut s'écrire ainsi:
a¯=dv¯/dt.
Évidemment, en prenant la dérivée seconde devecteur de déplacement l¯ dans le temps, on obtiendra aussi la valeur de l'accélération.
Comme la vitesse se mesure en mètres par seconde, l'accélération, selon l'expression écrite, se mesure en mètres par seconde au carré.

Où sont les vecteurs accélération et vitesse ?
En physique, tout mouvement mécanique d'un corps est généralement caractérisé par une certaine trajectoire. Ce dernier est une courbe imaginaire le long de laquelle le corps se déplace dans l'espace. Par exemple, une ligne droite ou un cercle sont d'excellents exemples de trajectoires de mouvement courantes.
Le vecteur vitesse du corps est toujours dirigé dans la direction du mouvement, que le corps ralentisse ou accélère, qu'il se déplace en ligne droite ou le long d'une courbe. En termes géométriques, le vecteur vitesse est dirigé tangentiellement au point de la trajectoire où se trouve actuellement le corps.
Le vecteur d'accélération d'un matériau ou d'un point du corps n'a rien à voir avec la vitesse. Ce vecteur est dirigé dans le sens du changement de vitesse. Par exemple, pour un mouvement rectiligne, la valeur a¯ peut soit coïncider en direction avec v¯ soit être opposée à v¯.
Force agissant sur le corps et accélération
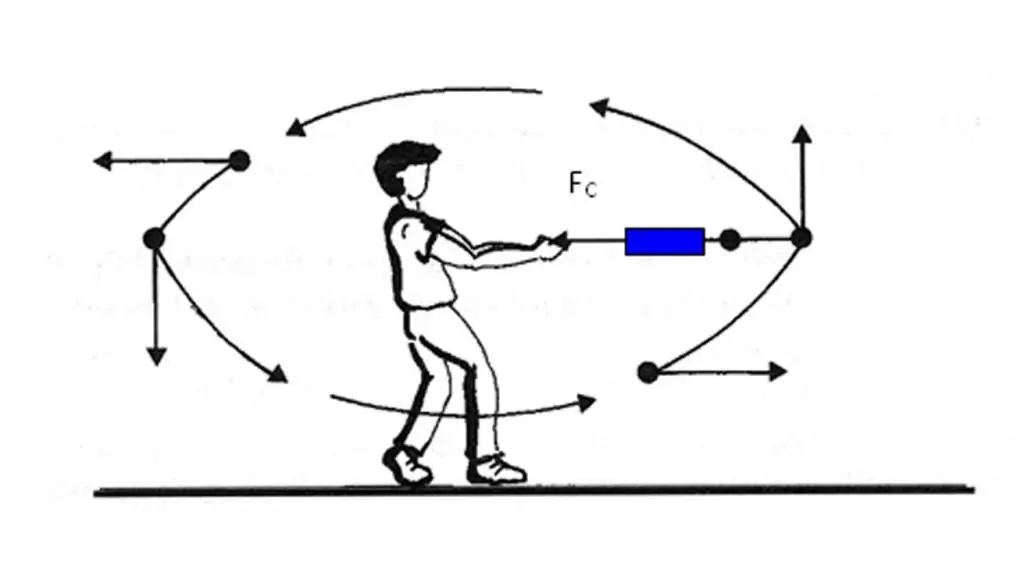
Nous avons découvert que le vecteur accélération du corps est dirigé vers le changement du vecteur vitesse. Cependant, il n'est pas toujours aisé de déterminer l'évolution de la vitesse en un point donné de la trajectoire. De plus, pour déterminer le changement de vitesse, il est nécessaire d'effectuer l'opérationdifférences vectorielles. Pour éviter ces difficultés de détermination de la direction du vecteur a¯, il existe un autre moyen de le savoir rapidement.
Ci-dessous se trouve la loi de Newton célèbre et bien connue de tous les étudiants:
F¯=ma¯.
La formule montre que la cause de l'accélération dans les corps est la force qui agit sur eux. Comme la masse m est un scalaire, le vecteur force F¯ et le vecteur accélération a¯ sont dans la même direction. Ce fait doit être rappelé et appliqué dans la pratique chaque fois qu'il est nécessaire de déterminer la direction de la quantité a¯.
Si plusieurs forces différentes agissent sur le corps, alors la direction du vecteur d'accélération sera égale au vecteur résultant de toutes les forces.
Mouvement circulaire et accélération
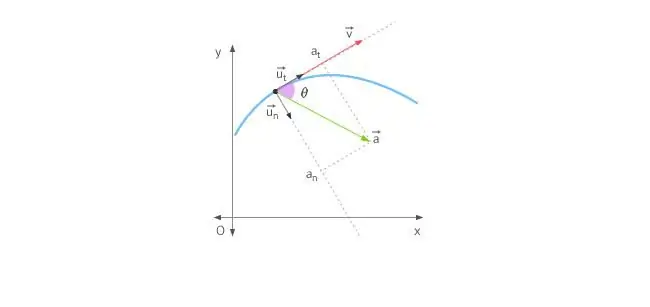
Lorsqu'un corps se déplace en ligne droite, l'accélération est dirigée vers l'avant ou vers l'arrière. Dans le cas d'un mouvement circulaire, la situation est compliquée par le fait que le vecteur vitesse change constamment de direction. Compte tenu de ce qui précède, l'accélération totale est déterminée par ses deux composantes: les accélérations tangentielle et normale.
L'accélération tangentielle est dirigée exactement de la même manière que le vecteur vitesse, ou contre lui. En d'autres termes, cette composante d'accélération est dirigée selon la tangente à la trajectoire. L'accélération tangentielle décrit le changement du module de la vitesse elle-même.
L'accélération normale est dirigée le long de la normale au point donné de la trajectoire, en tenant compte de sa courbure. Dans le cas d'un mouvement circulaire, le vecteur de cette composante indiqueau centre, c'est-à-dire que l'accélération normale est dirigée le long du rayon de rotation. Cette composante est souvent appelée centripète.
L'accélération complète est la somme de ces composantes, donc son vecteur peut être dirigé arbitrairement par rapport à la ligne du cercle.
Si le corps tourne sans changer la vitesse linéaire, alors il n'y a qu'une composante normale non nulle, donc le vecteur d'accélération complet est dirigé vers le centre du cercle. Notez que ce centre est également affecté par une force qui maintient le corps sur sa trajectoire. Par exemple, la force gravitationnelle du Soleil maintient notre Terre et les autres planètes sur leurs orbites.






