Le module d'élasticité est une grandeur physique qui caractérise le comportement élastique d'un matériau lorsqu'une force externe lui est appliquée dans une direction particulière. Le comportement élastique d'un matériau signifie sa déformation dans la région élastique.
Histoire de l'étude de l'élasticité des matériaux

La théorie physique des corps élastiques et leur comportement sous l'action de forces extérieures ont été examinées en détail et étudiées par le scientifique anglais du 19ème siècle, Thomas Young. Cependant, le concept même d'élasticité a été développé dès 1727 par le mathématicien, physicien et philosophe suisse Leonhard Euler, et les premières expériences liées au module d'élasticité ont été réalisées en 1782, soit 25 ans avant les travaux de Thomas Jung., par le mathématicien et philosophe vénitien Jacopo Ricatti.
Thomas Young a le mérite d'avoir donné à la théorie de l'élasticité une allure moderne et élancée, formalisée par la suite sous la forme d'une loi de Hooke simple puis généralisée.
Nature physique de l'élasticité
Tout corps est constitué d'atomes, entre lesquels agissent les forces d'attraction et de répulsion. L'équilibre de ces forces estl'état et les paramètres de la matière dans des conditions données. Les atomes d'un corps solide, lorsque des forces externes de tension ou de compression insignifiantes leur sont appliquées, commencent à se déplacer, créant une force opposée en direction et égale en amplitude, qui tend à ramener les atomes à leur état initial.
Dans le processus d'un tel déplacement d'atomes, l'énergie de l'ensemble du système augmente. Les expériences montrent qu'aux petites déformations, l'énergie est proportionnelle au carré de ces déformations. Cela signifie que la force, étant une dérivée par rapport à l'énergie, s'avère être proportionnelle à la première puissance de la déformation, c'est-à-dire qu'elle en dépend linéairement. En répondant à la question, quel est le module d'élasticité, nous pouvons dire que c'est le coefficient de proportionnalité entre la force agissant sur l'atome et la déformation que cette force provoque. La dimension du module de Young est la même que la dimension de la pression (Pascal).
Limite élastique
Selon la définition, le module d'élasticité indique la quantité de contrainte qui doit être appliquée à un solide pour que sa déformation soit de 100 %. Cependant, tous les solides ont une limite d'élasticité égale à 1 % de déformation. Cela signifie que si une force appropriée est appliquée et que le corps est déformé d'une quantité inférieure à 1%, alors après la fin de cette force, le corps restaure exactement sa forme et ses dimensions d'origine. Si trop de force est appliquée, à laquelle la valeur de déformation dépasse 1%, après la fin de la force externe, le corps ne retrouvera plus ses dimensions d'origine. Dans ce dernier cas, on parle de l'existence d'une déformation résiduelle, qui estpreuve que la limite élastique du matériau a été dépassée.
Module de Young en action
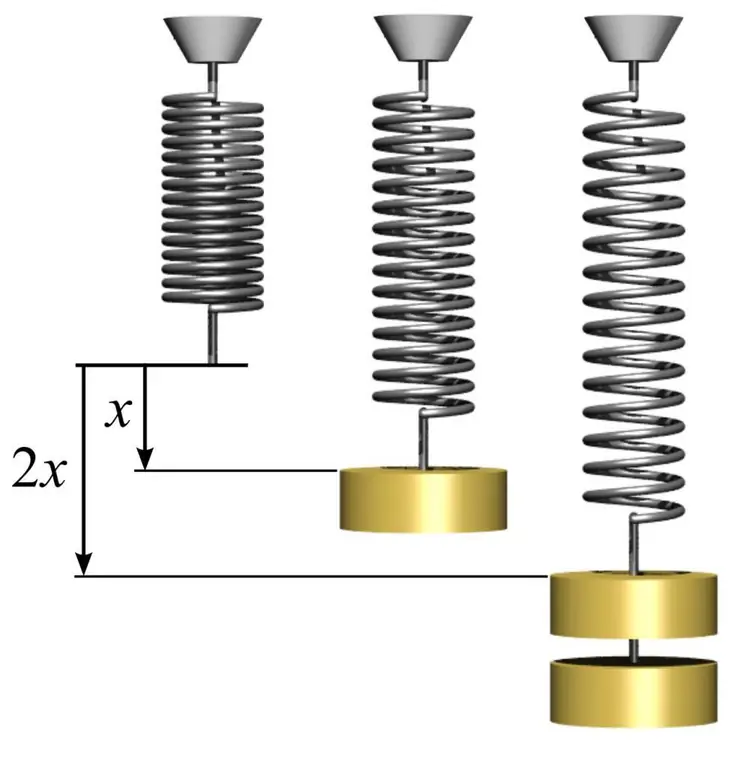
Pour déterminer le module d'élasticité, ainsi que pour comprendre comment l'utiliser, vous pouvez donner un exemple simple avec un ressort. Pour ce faire, vous devez prendre un ressort métallique et mesurer l'aire du cercle formé par ses bobines. Ceci est fait en utilisant la formule simple S=πr², où n est pi égal à 3,14 et r est le rayon de la spire du ressort.
Ensuite, mesurer la longueur du ressort l0 sans charge. Si vous suspendez une charge de masse m1 sur un ressort, sa longueur augmentera jusqu'à une certaine valeur l1. Le module d'élasticité E peut être calculé sur la base de la connaissance de la loi de Hooke par la formule: E=m1gl0/(S(l 1-l0)), où g est l'accélération de la chute libre. Dans ce cas, nous notons que la quantité de déformation du ressort dans la région élastique peut largement dépasser 1 %.
Connaître le module de Young permet de prédire la quantité de déformation sous l'action d'une contrainte particulière. Dans ce cas, si on accroche une autre masse m2 au ressort, on obtient la valeur de déformation relative suivante: d=m2g/ (SE), où d - déformation relative dans la région élastique.
Isotropie et anisotropie
Le module d'élasticité est une caractéristique d'un matériau qui décrit la force de la liaison entre ses atomes et ses molécules, mais un matériau particulier peut avoir plusieurs modules de Young différents.
Le fait est que les propriétés de chaque solide dépendent de sa structure interne. Si les propriétés sont les mêmes dans toutes les directions spatiales, on parle alors d'un matériau isotrope. Ces substances ont une structure homogène, de sorte que l'action d'une force externe dans différentes directions sur elles provoque la même réaction du matériau. Tous les matériaux amorphes sont isotropes, comme le caoutchouc ou le verre.
L'anisotropie est un phénomène caractérisé par la dépendance des propriétés physiques d'un solide ou d'un liquide à la direction. Tous les métaux et alliages basés sur eux ont l'un ou l'autre réseau cristallin, c'est-à-dire un arrangement ordonné plutôt que chaotique de noyaux ioniques. Pour de tels matériaux, le module d'élasticité varie en fonction de l'axe d'action de la contrainte externe. Par exemple, les métaux à symétrie cubique, tels que l'aluminium, le cuivre, l'argent, les métaux réfractaires et autres, ont trois modules de Young différents.
Module de cisaillement
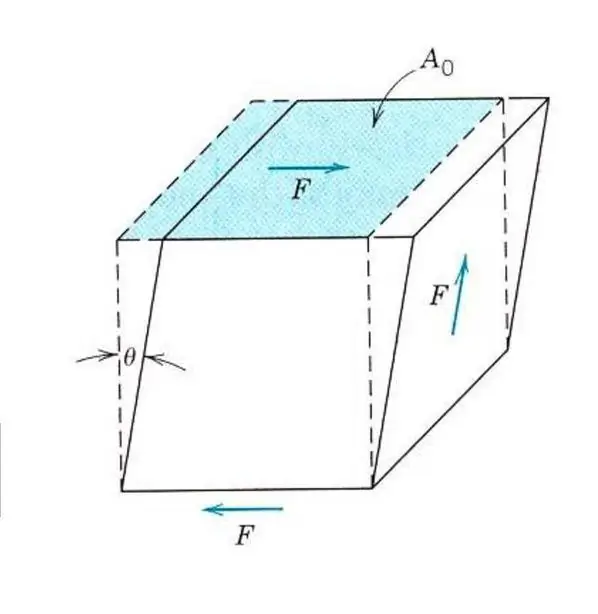
Description des propriétés élastiques d'un matériau même isotrope ne nécessite pas la connaissance d'un module de Young. Car, en plus de la traction et de la compression, le matériau peut être affecté par des contraintes de cisaillement ou de torsion. Dans ce cas, il réagira différemment à la force extérieure. Pour décrire la déformation élastique par cisaillement, un analogue du module de Young, du module de cisaillement ou du module d'élasticité de deuxième espèce est introduit.
Tous les matériaux résistent moins aux contraintes de cisaillement qu'à la traction ou à la compression, de sorte que leur module de cisaillement est 2 à 3 fois inférieur à la valeur du module de Young. Ainsi, pour le titane, dont le module d'Young est égal à 107 GPa, le module de cisaillement estseulement 40 GPa, pour l'acier ces chiffres sont respectivement de 210 GPa et 80 GPa.
Module d'élasticité du bois

Le bois est un matériau anisotrope car les fibres de bois sont orientées dans une direction spécifique. C'est le long des fibres que le module d'élasticité du bois est mesuré, car il est inférieur de 1 à 2 ordres de grandeur à travers les fibres. La connaissance du module de Young du bois est importante et est prise en compte lors de la conception des structures en panneaux de bois.
Les valeurs du module d'élasticité du bois pour certains types d'arbres sont indiquées dans le tableau ci-dessous.
| Arborescence | Module de Young en GPa |
| Laurier | 14 |
| Eucalyptus | 18 |
| Cèdre | 8 |
| épicéa | 11 |
| Pin | 10 |
| Chêne | 12 |
Il convient de noter que les valeurs données peuvent différer jusqu'à 1 GPa pour un arbre particulier, car son module de Young est affecté par la densité du bois et les conditions de croissance.

Les modules de cisaillement pour diverses espèces d'arbres sont de l'ordre de 1 à 2 GPa, par exemple, pour le pin, il est de 1,21 GPa et pour le chêne de 1,38 GPa, c'est-à-dire que le bois ne résiste pratiquement pas aux contraintes de cisaillement. Ce fait doit être pris en compte dans la fabrication des structures porteuses en bois, qui sont conçues pour fonctionner uniquement en traction ou en compression.
Caractéristiques élastiques des métaux
En comparaison avec le module de Young du bois, les valeurs moyennes de cette valeur pour les métaux et alliages sont d'un ordre de grandeur supérieur, comme le montre le tableau suivant.
| Métal | Module de Young en GPa |
| Bronze | 120 |
| Cuivre | 110 |
| Acier | 210 |
| Titane | 107 |
| Nickel | 204 |
Les propriétés élastiques des métaux qui ont une syngonie cubique sont décrites par trois constantes élastiques. Ces métaux comprennent le cuivre, le nickel, l'aluminium, le fer. Si un métal a une syngonie hexagonale, alors six constantes sont déjà nécessaires pour décrire ses caractéristiques élastiques.
Pour les systèmes métalliques, le module de Young est mesuré à moins de 0,2 % de déformation, car des valeurs élevées peuvent déjà se produire dans la région inélastique.






