La loi d'Ohm est la loi fondamentale des circuits électriques. En même temps, cela nous permet d'expliquer de nombreux phénomènes naturels. Par exemple, on peut comprendre pourquoi l'électricité ne « bat » pas les oiseaux assis sur les fils. Pour la physique, la loi d'Ohm est extrêmement importante. Sans sa connaissance, il serait impossible de créer des circuits électriques stables ou il n'y aurait pas d'électronique du tout.
Dépendance I=I(U) et sa valeur
L'histoire de la découverte de la résistance des matériaux est directement liée à la caractéristique courant-tension. Ce que c'est? Prenons un circuit à courant électrique constant et considérons n'importe lequel de ses éléments: une lampe, un tuyau de gaz, un conducteur métallique, une fiole d'électrolyte, etc.
En modifiant la tension U (souvent appelée V) fournie à l'élément en question, nous suivrons l'évolution de l'intensité du courant (I) qui le traverse. En conséquence, nous obtiendrons une dépendance de la forme I \u003d I (U), qui s'appelle la "caractéristique de tension de l'élément" et est un indicateur direct de sapropriétés électriques.
La caractéristique V/A peut sembler différente pour différents éléments. Sa forme la plus simple est obtenue en considérant un conducteur métallique, ce qui fut fait par Georg Ohm (1789 - 1854).
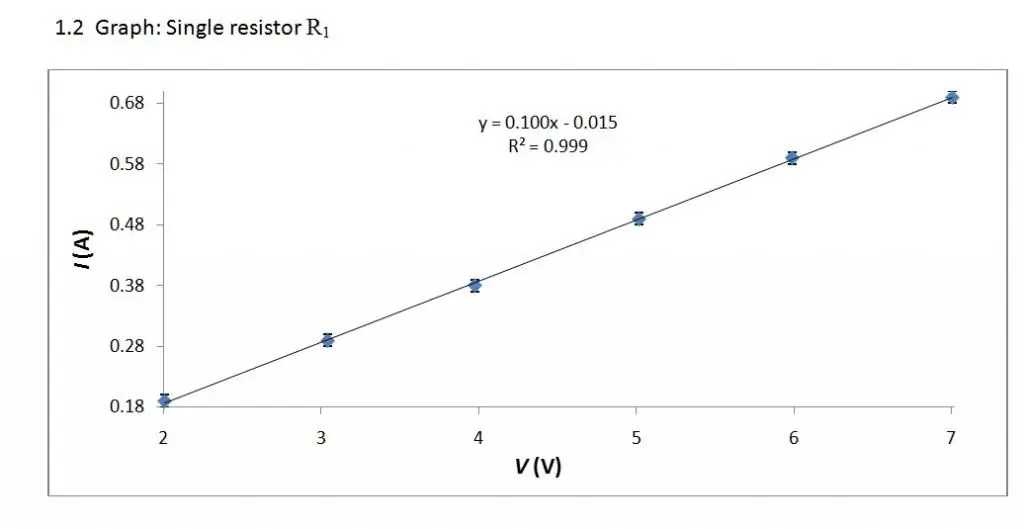
La caractéristique volt-ampère est une relation linéaire. Par conséquent, son graphique est une ligne droite.
La loi dans sa forme la plus simple
Les recherches d'Ohm sur les caractéristiques courant-tension des conducteurs ont montré que l'intensité du courant à l'intérieur d'un conducteur métallique est proportionnelle à la différence de potentiel à ses extrémités (I ~ U) et inversement proportionnelle à un certain coefficient, c'est-à-dire I ~ 1/R. Ce coefficient est devenu connu sous le nom de "résistance du conducteur", et l'unité de mesure de la résistance électrique était Ohm ou V/A.
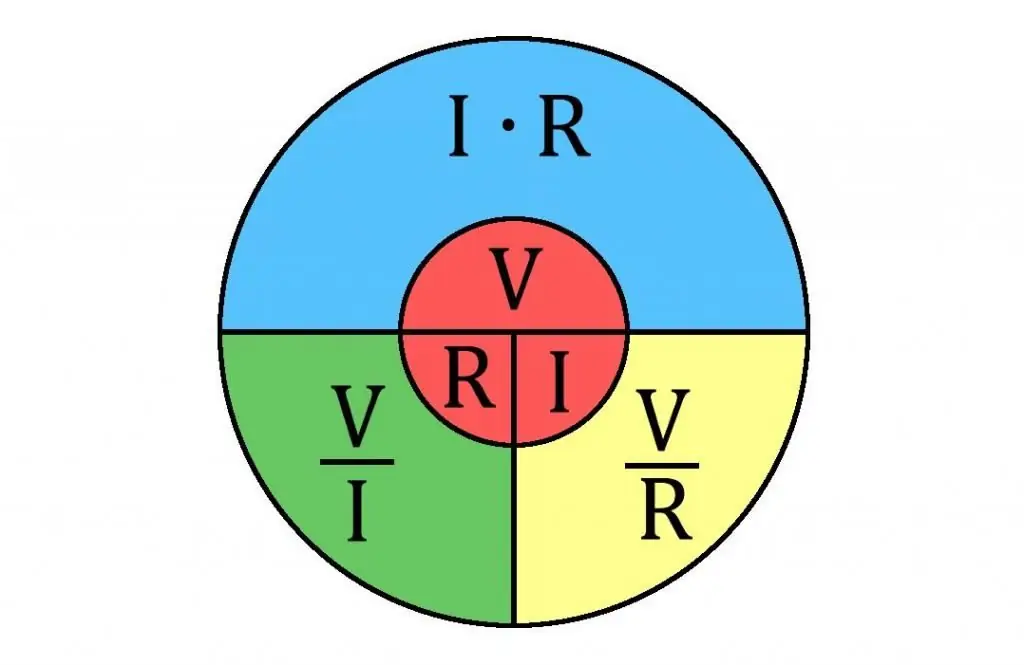
Encore une chose à noter. La loi d'Ohm est souvent utilisée pour calculer la résistance dans les circuits.
Libellé de la loi
La loi d'Ohm dit que l'intensité du courant (I) d'une seule section du circuit est proportionnelle à la tension dans cette section et inversement proportionnelle à sa résistance.
Il convient de noter que sous cette forme la loi ne reste vraie que pour une section homogène de la chaîne. Homogène est la partie du circuit électrique qui ne contient pas de source de courant. Comment utiliser la loi d'Ohm dans un circuit non homogène sera discuté ci-dessous.
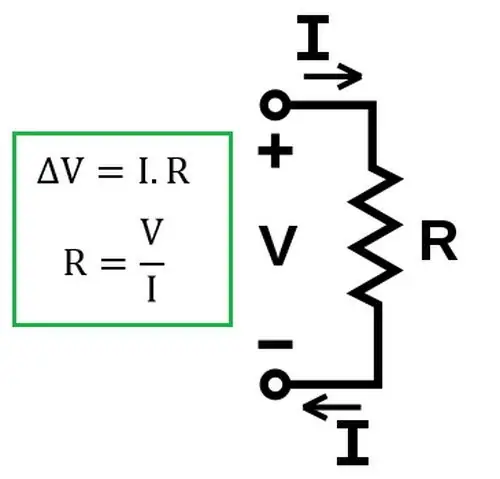
Plus tard, il a été expérimentalement établi que la loi reste valable pour les solutionsélectrolytes dans un circuit électrique.
Signification physique de la résistance
La résistance est une propriété des matériaux, des substances ou des médias pour empêcher le passage du courant électrique. Quantitativement, une résistance de 1 ohm signifie que dans un conducteur avec une tension de 1 V à ses extrémités, un courant électrique de 1 A peut passer.
Résistivité électrique
Expérimentalement, il a été constaté que la résistance du courant électrique du conducteur dépend de ses dimensions: longueur, largeur, hauteur. Et aussi sur sa forme (sphère, cylindre) et le matériau dont il est fait. Ainsi, la formule de résistivité, par exemple, d'un conducteur cylindrique homogène sera: R \u003d pl / S.
Si dans cette formule on pose s=1 m2 et l=1 m, alors R sera numériquement égal à p. À partir de là, l'unité de mesure du coefficient de résistivité du conducteur en SI est calculée - c'est Ohmm.

Dans la formule de résistivité, p est le coefficient de résistance déterminé par les propriétés chimiques du matériau à partir duquel le conducteur est fabriqué.
Pour considérer la forme différentielle de la loi d'Ohm, nous devons considérer quelques concepts supplémentaires.
Densité de courant
Comme vous le savez, le courant électrique est un mouvement strictement ordonné de toute particule chargée. Par exemple, dans les métaux, les porteurs de courant sont les électrons, et dans les gaz conducteurs, les ions.
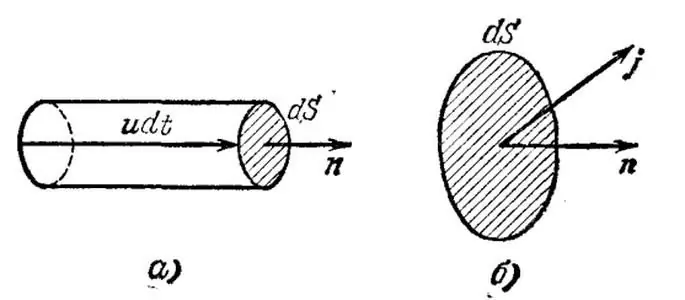
Prenons le cas trivial lorsque tous les opérateurs actuelshomogène - conducteur métallique. Distinguons mentalement un volume infiniment petit dans ce conducteur et notons u la vitesse moyenne (dérive, ordonnée) des électrons dans le volume donné. En outre, notons n la concentration de porteurs de courant par unité de volume.
Traçons maintenant une aire infinitésimale dS perpendiculaire au vecteur u et construisons le long de la vitesse un cylindre infinitésimal de hauteur udt, où dt désigne le temps pendant lequel tous les porteurs de vitesse courants contenus dans le volume considéré passeront à travers la zone dS.
Dans ce cas, la charge égale à q=neudSdt sera transférée par les électrons à travers la zone, où e est la charge de l'électron. Ainsi, la densité de courant électrique est un vecteur j=neu, indiquant la quantité de charge transférée par unité de temps à travers une unité de surface.
L'un des avantages de la définition différentielle de la loi d'Ohm est que vous pouvez souvent vous débrouiller sans calculer la résistance.
Charge électrique. Intensité du champ électrique
L'intensité du champ avec la charge électrique est un paramètre fondamental de la théorie de l'électricité. En même temps, une idée quantitative de ceux-ci peut être obtenue à partir d'expériences simples à la disposition des écoliers.
Pour simplifier, nous allons considérer un champ électrostatique. C'est un champ électrique qui ne change pas avec le temps. Un tel champ peut être créé par des charges électriques stationnaires.
En outre, une charge de test est nécessaire pour nos besoins. Dans sa capacité, nous utiliserons un corps chargé - si petit qu'il n'est pas capable de provoquertoute perturbation (redistribution des charges) dans les objets environnants.
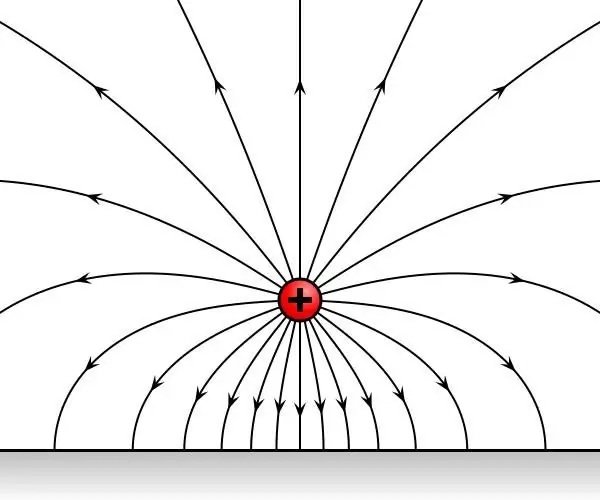
Considérons tour à tour deux charges d'essai prises, placées successivement en un point de l'espace, qui est sous l'influence d'un champ électrostatique. Il s'avère que les charges seront soumises à une influence invariante dans le temps de sa part. Soient F1 et F2 les forces agissant sur les charges.
À la suite de la généralisation des données expérimentales, il a été constaté que les forces F1 et F2 sont dirigées soit dans un ou dans des directions opposées, et leur rapport F1/F2 est indépendant du point de l'espace où les charges d'essai ont été alternativement placées. Par conséquent, le rapport F1/F2 est une caractéristique des charges elles-mêmes et ne dépend pas du champ.
La découverte de ce fait a permis de caractériser l'électrisation des corps et fut plus tard appelée charge électrique. Ainsi, par définition, il s'avère q1/q2=F1/F 2 , où q1 et q2 - le montant des charges placées en un point du terrain, et F 1 et F2 - forces agissant sur les charges depuis le côté du terrain.
À partir de ces considérations, les grandeurs des charges de diverses particules ont été établies expérimentalement. En définissant conditionnellement l'une des charges de test égale à un dans le rapport, vous pouvez calculer la valeur de l'autre charge en mesurant le rapport F1/F2.
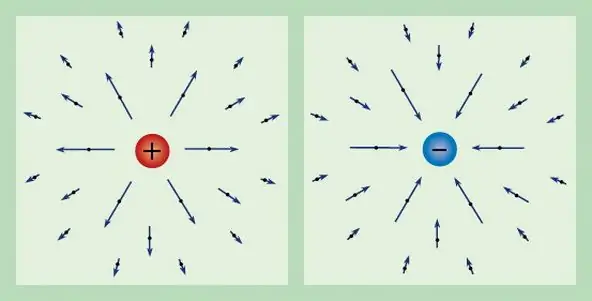
Tout champ électrique peut être caractérisé par une charge connue. Ainsi, la force agissant sur une charge unitaire d'essai au repos est appelée l'intensité du champ électrique et est notée E. De la définition de la charge, on obtient que le vecteur d'intensité a la forme suivante: E=F/q.
Connexion des vecteurs j et E. Une autre forme de la loi d'Ohm
Dans un conducteur homogène, le mouvement ordonné des particules chargées se produira dans la direction du vecteur E. Cela signifie que les vecteurs j et E seront co-dirigés. Comme pour déterminer la densité de courant, nous sélectionnons un volume cylindrique infiniment petit dans le conducteur. Alors un courant égal à jdS traversera la section transversale de ce cylindre, et la tension appliquée au cylindre sera égale à Edl. La formule de la résistivité d'un cylindre est également connue.
Ensuite, en écrivant la formule de l'intensité du courant de deux manières, nous obtenons: j=E/p, où la valeur 1/p est appelée conductivité électrique et est l'inverse de la résistivité électrique. Il est généralement noté σ (sigma) ou λ (lambda). L'unité de conductivité est Sm/m, où Sm est Siemens. Unité inverse de Ohm.
Ainsi, nous pouvons répondre à la question posée ci-dessus sur la loi d'Ohm pour un circuit non homogène. Dans ce cas, les porteurs de courant seront affectés par la force du champ électrostatique, qui est caractérisée par l'intensité E1, et d'autres forces agissant sur eux à partir d'une autre source de courant, qui peut être désigné E 2. Ensuite, la loi d'Ohm s'est appliquée àsection non homogène de la chaîne ressemblera à: j=λ(E1 + E2).
En savoir plus sur la conductivité et la résistance
La capacité d'un conducteur à conduire un courant électrique est caractérisée par sa résistivité, qui peut être trouvée grâce à la formule de résistivité, ou conductivité, calculée comme l'inverse de la conductivité. La valeur de ces paramètres est déterminée à la fois par les propriétés chimiques du matériau conducteur et par les conditions extérieures. En particulier, la température ambiante.
Pour la plupart des métaux, la résistivité à température normale lui est proportionnelle, c'est-à-dire p ~ T. Cependant, des écarts sont observés à basse température. Pour un grand nombre de métaux et alliages à des températures proches de 0°K, le calcul de résistance a montré des valeurs nulles. Ce phénomène est appelé supraconductivité. Par exemple, le mercure, l'étain, le plomb, l'aluminium, etc… ont cette propriété. Chaque métal a sa propre température critique Tk, à laquelle le phénomène de supraconductivité est observé.
Notez également que la définition de la résistivité du cylindre peut être généralisée aux fils constitués du même matériau. Dans ce cas, la section transversale de la formule de résistivité sera égale à la section transversale du fil et l - sa longueur.






