La règle de Titius-Bode (parfois simplement appelée loi de Bode) est l'hypothèse selon laquelle les corps de certains systèmes orbitaux, dont le Soleil, tournent le long de demi-axes en fonction de la séquence planétaire. La formule suggère qu'en s'étendant vers l'extérieur, chaque planète sera environ deux fois plus éloignée du Soleil que la précédente.
L'hypothèse a correctement prédit les orbites de Cérès (dans la ceinture d'astéroïdes) et d'Uranus, mais n'a pas réussi à déterminer l'orbite de Neptune et a finalement été remplacée par la théorie de la formation du système solaire. Il porte le nom de Johann Daniel Titius et Johann Elert Bode.

Origines
La première mention d'une série se rapprochant de la loi de Bode se trouve dans Elements of Astronomy de David Gregory, publié en 1715. Il y dit: "… en supposant que la distance du Soleil à la Terre est divisée en dix parties égales, dont la distance de Mercure sera d'environ quatre, de Vénus sept, de Mars quinze, de Jupiter cinquante-deux, et de Saturne quatre-vingt-quinze". Une suggestion similaire, probablement inspirée par Gregory, apparaît dans un ouvrage publié par Christian Wolff en 1724.
En 1764, Charles Bonnet, dans son livre Contemplation de la nature, disait: "Nous connaissons les dix-sept planètes qui composent notre système solaire [c'est-à-dire les planètes principales et leurs satellites], mais nous ne sommes pas sûrs que ils ne sont plus." À cela, dans sa traduction de 1766 de l'œuvre de Bonnet, Johann Daniel Titius ajouta deux paragraphes de son cru en bas de la page 7 et en haut de la page 8. Le nouveau paragraphe interpolé ne se trouve pas dans le texte original de Bonnet: ni dans l'italien ni les traductions anglaises de l'œuvre.
Découverte de Titius
Il y a deux parties dans le texte intercalé de Titius. Le premier explique la séquence des distances planétaires au Soleil. Il contient également quelques mots sur la distance du Soleil à Jupiter. Mais ce n'est pas la fin du texte.
Il vaut la peine de dire quelques mots sur la formule de la règle de Titius-Bode. Faites attention aux distances entre les planètes et découvrez que presque toutes sont séparées les unes des autres dans une proportion correspondant à leur taille corporelle. Divisez la distance du Soleil à Saturne par 100 parties; puis Mercure est séparé par quatre de ces parties du Soleil; Vénus - en 4 + 3=7 de ces parties; Terre - par 4+6=10; Mars - par 4+12=16.
Mais notez que de Mars à Jupiter il y a un écart par rapport à cette progression si précise. Un espace de 4+24=28 de ces parties découle de Mars, mais jusqu'à présent aucune planète n'y a été découverte. Mais le Seigneur Architecte devrait-il laisser cet endroit vide ? Jamais. Alorssupposons que cet espace appartient sans aucun doute aux lunes encore inconnues de Mars, et ajoutons que peut-être Jupiter a encore quelques lunes plus petites autour de lui qui n'ont encore été vues par aucun télescope.

Rise of the Bode
En 1772, Johann Elert Bode, à l'âge de vingt-cinq ans, termine la deuxième édition de son recueil astronomique Anleitung zur Kenntniss des gestirnten Himmels ("Guide pour la connaissance du ciel étoilé"), auquel il a ajouté la note de bas de page suivante, à l'origine sans source, mais notée dans les versions ultérieures. Dans les mémoires de Bode, on peut trouver une référence à Titius avec une reconnaissance claire de son autorité.

Opinion Bode
C'est ainsi que résonne la règle de Titius-Bode dans la présentation de ce dernier: si la distance du Soleil à Saturne est prise égale à 100, alors Mercure est séparé du Soleil par quatre de ces parties. Vénus - 4+3=7. Terre - 4+6=10. Mars - 4+12=16.
Maintenant, il y a un vide dans cette progression ordonnée. Après Mars suit un espace avec un calcul de 4+24=28, dans lequel pas une seule planète n'a encore été vue. Pouvons-nous croire que le Fondateur de l'univers a laissé cet espace vide ? Bien sûr que non. De là, nous arrivons à la distance de Jupiter sous la forme de calcul 4+48=52 et, enfin, à la distance de Saturne - 4+96=100.

Ces deux déclarations concernant toutes les typologies spécifiques et les rayons orbitaux semblent provenir de l'ancienneastronomie. Beaucoup de ces théories datent d'avant le XVIIe siècle.
Influence
Titius était l'élève du philosophe allemand Christian Freiherr von Wolff (1679-1754). La deuxième partie du texte inséré dans l'œuvre de Bonnet est basée sur l'œuvre de 1723 de von Wolff, Vernünftige Gedanken von den Wirkungen der Natur.
La littérature du XXe siècle attribue la paternité de la règle de Titius-Bode à un philosophe allemand. Si oui, Titius pourrait apprendre de lui. Une autre référence plus ancienne a été écrite par James Gregory en 1702 dans son Astronomiae Physicae et geometryae Elementa, où la séquence des distances planétaires 4, 7, 10, 16, 52 et 100 est devenue une progression géométrique du rapport 2.
C'est la formule la plus proche de Newton, et a également été trouvée dans les écrits de Benjamin Martin et Thomas Ceard des années avant la publication du livre de Bonnet en Allemagne.
Poursuite des travaux et implications pratiques
Titius et Bode espéraient que la loi conduirait à la découverte de nouvelles planètes, et en effet, la découverte d'Uranus et de Cérès, dont la distance s'accorde bien avec la loi, a contribué à son acceptation par le monde scientifique.
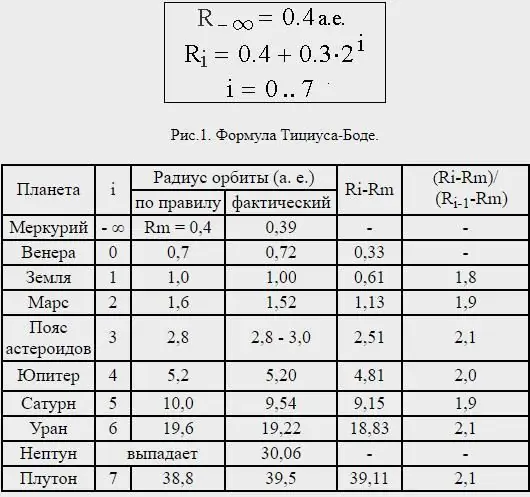
Cependant, la distance de Neptune était très incohérente, et en fait Pluton - qui n'est plus considérée comme une planète - se trouve à une distance moyenne qui correspond à peu près à la loi de Titius-Bode prédite pour la prochaine planète en dehors d'Uranus.
La loi initialement publiée était approximativement satisfaite par toutes les planètes connues - Mercure et Saturne - avec un écart entrequatrième et cinquième planètes. Ce chiffre était considéré comme intéressant, mais pas d'une grande importance, jusqu'à la découverte d'Uranus en 1781, qui s'inscrit dans la série.
Sur la base de cette découverte, Bode a appelé à la recherche d'une cinquième planète. Cérès, le plus gros objet de la ceinture d'astéroïdes, a été trouvé à la position prédite par Bode en 1801. La loi de Bode a été largement acceptée jusqu'à la découverte de Neptune en 1846 et s'est avérée incompatible avec la loi.
Dans le même temps, un grand nombre d'astéroïdes découverts dans la ceinture ont rayé Cérès de la liste des planètes. La loi de Bode a été discutée par l'astronome et logicien Charles Sanders Peirce en 1898 comme un exemple de raisonnement fallacieux.

Développement du problème
La découverte de Pluton en 1930 a encore compliqué le problème. Même si cela ne correspondait pas à la position prédite par la loi de Bode, il s'agissait de la position prédite par la loi pour Neptune. Cependant, la découverte ultérieure de la ceinture de Kuiper, et en particulier de l'objet Eris, qui est plus massif que Pluton mais n'est pas conforme à la loi de Bode, a encore discrédité la formule.
Contribution de Serda
Le jésuite Thomas Cerda a donné le célèbre cours d'astronomie à Barcelone en 1760 à la Chaire Royale de Mathématiques du Collège de Sant Jaume de Cordelle (Séminaire Impérial et Royal des Nobles de Cordell). Dans le Tratado de Cerdas apparaissent les distances planétaires, obtenues en appliquant la troisième loi de Kepler, avec une précision de 10-3.
Si nous prenons comme 10 la distance de la Terre etarrondi à l'entier supérieur, la progression géométrique [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, de n=2 à n=8, peut être exprimée. Et en utilisant un mouvement fictif uniforme circulaire à l'anomalie de Kepler, les valeurs Rn correspondant aux rapports de chaque planète peuvent être obtenues comme rn=(Rn - R1) / (Rn-1 - R1), ce qui donne 1,82; 1, 84; 1, 86; 1.88 et 1.90, où rn=2 - 0.02 (12 - n) est une relation explicite entre la continuité de Kepler et la loi de Titius-Bode, qui est considérée comme une coïncidence numérique aléatoire. Le résultat du calcul est proche de deux, mais le deux peut très bien être considéré comme un arrondi du nombre 1, 82.

La vitesse moyenne de la planète de n=1 à n=8 réduit la distance du Soleil et diffère du déclin uniforme à n=2 pour récupérer à partir de n=7 (résonance orbitale). Cela affecte la distance du Soleil à Jupiter. Cependant, la distance entre tous les autres objets dans le cadre de la règle notoire à laquelle l'article est consacré est également déterminée par cette dynamique mathématique.
Aspect théorique
Il n'y a pas d'explication théorique solide sous-jacente à la règle de Titius-Bode, mais il est possible qu'étant donné la combinaison de la résonance orbitale et du manque de degrés de liberté, tout système planétaire stable ait une forte probabilité de répéter le modèle décrit dans cette théorie par les deux scientifiques.
Parce que cela peut être une coïncidence mathématique et non une "loi de la nature", on l'appelle parfois une règle plutôt qu'une "loi". Cependant, l'astrophysicien Alan Boss soutient qu'il s'agit simplementcoïncidence, et la revue scientifique planétaire Icarus n'accepte plus les articles tentant de fournir des versions améliorées de la "loi".
Résonance orbitale
La résonance orbitale des principaux corps en orbite crée des régions autour du Soleil qui n'ont pas d'orbites stables à long terme. Les résultats de la simulation de la formation des planètes soutiennent l'idée qu'un système planétaire stable choisi au hasard est susceptible de satisfaire la règle de Titius-Bode.

Dubrulle et Graner
Dubrulle et Graner ont montré que les règles de distance de la loi de puissance peuvent être une conséquence de modèles d'effondrement de nuages de systèmes planétaires qui ont deux symétries: l'invariance de rotation (le nuage et son contenu sont axisymétriques) et l'invariance d'échelle (le nuage et son contenu est le même à toutes les échelles).
Ce dernier est une caractéristique de nombreux phénomènes censés jouer un rôle dans la formation des planètes, comme la turbulence. La distance du Soleil aux planètes du système solaire, proposée par Titius et Bode, n'a pas été révisée dans le cadre des études de Dubrulle et Graner.






